Imagine Álgebra Linear. Adição, Multiplição de Matrizes. Sistemas de Equações Lineares. Inversões de Matrizes. Decomposições de Matrizes. Autovalores, Autovetores e Valores Singulares. Eu pessoalmente acredito que o inferno deve ser um lugar que as pessoas são obrigadas a fazer cálculos de álgebra linear na mão! POR TODA A ETERNIDADE!1.
Caso você não saiba, o computador não foi criado para assistir pornografia para envio de e-mails, navegação na internet, ou games. Mas sim para operações e manipulações de matrizes! Shayle Searle no livro Matrix Algebra Useful for Statistics recorda que, durante seus anos de estudante de doutorado em 1959 na Cornell University, ele e seus colegas ficaram impressionados quando conseguiram inverter uma matriz de dimensão 10 x 10 em 7 minutos num computador. Searle também recorda que um ano antes, um colega inverteu uma matriz de dimensão 40 x 40 usando uma calculadora elétrica. Ele demorou 6 semanas!
Nesse tutorial vou mostrar como usar o básico das bibliotecas C++ Eigen e Armadillo. Ambas fazem a mesma coisa: Álgebra Linear e Manipulação de Matrizes e Vetores. Elas diferem (além da síntaxe) em uma coisa:
Armadillodepende de LAPACK/BLAS/MKLEigennão possui nenhuma dependência
Além disso, em diversos benchmarks que eu fiz, Eigen (pelo menos no meu computador) é mais rápida que Armadillo. Esse tutorial apresentará primeiro Armadillo e a sua interface com R usando o {RcppArmadillo} e {Rcpp}. Na sequência apresentarei Eigen e sua interface com R usando o {RcppEigen} e {Rcpp}. Não se preocupe, qualquer uma das duas é literalmente “Álgebra Linear com Lasers”: são muito rápidas!

Figure 1: Qualquer escolha entre Armadillo e Eigen são bem rápidas: Álgebra Linear com Lasers!.
Armadillo
Armadillo é uma biblioteca de álgebra linear de alta qualidade para a linguagem C++, visando um bom equilíbrio entre velocidade e facilidade de uso. Ela fornece sintaxe deliberadamente semelhante ao Matlab. Caso você tenha experiência prévia com Matlab, use Armadillo e seja feliz. Veja em seu site mais informações sobre a biblioteca Armadillo. Além disso, recomendo as seguintes referências sobre Armadillo:
- Cheatsheet de síntaxe
ArmadillovsMatlab/Octavefeita pela própria equipe daArmadillo. - Site do pacote
{RcppArmadillo}que faz a interface entreRcppeArmadillo. - Cheatsheet de operações comuns de
{RcppArmadillo}pelo James Balamuta (também conhecido como TheCoatlessProfessor). - Documentação do
Armadillo
Classes do Armadillo
Armadillo possui algumas categorias de classes para representar diferentes objetos de álgebra linear:
Dense Matrix– Classes para matrizes densas (não-esparsas), com elementos armazenados em ordem de coluna principal (ou seja, coluna por coluna).mat = Mat<double> dmat = Mat<double> fmat = Mat<float> cx_mat = Mat<cx_double> // cx_ é Complex Numbers cx_dmat = Mat<cx_double> // cx_ é Complex Numbers cx_fmat = Mat<cx_float> // cx_ é Complex NumbersDense Vector– aqui se divide em vetores coluna (Column Vector) e vetores linha (Row Vector).Column Vector–Dense Matrixcom apenas uma única coluna.
vec = colvec = Col<double> dvec = dcolvec = Col<double> fvec = fcolvec = Col<float> cx_vec = cx_colvec = Col<cx_double> // cx_ é Complex Numbers cx_dvec = cx_dcolvec = Col<cx_double> // cx_ é Complex Numbers cx_fvec = cx_fcolvec = Col<cx_float> // cx_ é Complex NumbersRow Vector–Dense Matrixcom apenas uma única linha.
rowvec = Row<double> drowvec = Row<double> frowvec = Row<float> cx_rowvec = Row<cx_double> // cx_ é Complex Numbers cx_drowvec = Row<cx_double> // cx_ é Complex Numbers cx_frowvec = Row<cx_float> // cx_ é Complex NumbersSparse Matrix– Classes para matrizes esparsas; destina-se a armazenar matrizes muito grandes, onde a grande maioria dos elementos são zero.sp_mat = SpMat<double> sp_dmat = SpMat<double> sp_fmat = SpMat<float> sp_cx_mat = SpMat<cx_double> // cx_ é Complex Numbers sp_cx_dmat = SpMat<cx_double> // cx_ é Complex Numbers sp_cx_fmat = SpMat<cx_float> // cx_ é Complex Numbers
Como usar Armadillo com {Rcpp} – {RcppArmadillo}
Primeiro, certifique-se que você possui a biblioteca Armadillo instalada:
- Linux:
sudo apt-get install make libopenblas-dev liblapack-dev libarpack2-dev libsuperlu-dev - MacOS:
brew install armadillo - Windows: baixe no site do
Armadillo
Segundo, instale o pacote {RcppArmadillo} para R.
Terceiro, coloque em todo código que deseja usar o Armadillo com {Rcpp} a seguinte síntaxe:
#include <RcppArmadillo.h>
using namespace arma;
// [[Rcpp::depends(RcppArmadillo)]]Atenção!: não usar o header do {Rcpp} (#include <Rcpp.h>), pois ele conflita com o header do {RcppArmadillo} (#include <RcppArmadillo.h>).
Pronto! É isso.
Como usar Matrizes Esparsas no {RcppArmadillo}
O R possui um pacote {Matrix} que dá suporte à matrizes esparsas com uma classe dgCMatrix que significa double sparse Compressed Matrix. Veja um exemplo abaixo de uma matriz densa com 1,000,000 de elementos. Vamos enfiar alguns zeros nela de maneira aleatória. A matriz densa possui um tamanho de 7,6mb.
set.seed(123)
data <- rnorm(1e6)
zero_index <- sample(1e6)[1:9e5]
data[zero_index] <- 0
mat <- matrix(data, ncol=1000)
mat[1:5,1:5]
[,1] [,2] [,3] [,4] [,5]
[1,] 0.00 0 0 0 0
[2,] 0.00 0 0 0 0
[3,] 0.00 0 0 0 0
[4,] 0.00 0 0 0 0
[5,] 0.13 0 0 0 0print(object.size(mat), units = "auto")
7.6 MbAgora a mesma matriz mas armazenada como uma matriz esparsa pelo pacote {Matrix}. Note que os zeros foram eliminados da matriz (são armazenados de uma outra maneira) e o seu tamanho agora é 1,1mb.
5 x 5 sparse Matrix of class "dgCMatrix"
[1,] . . . . .
[2,] . . . . .
[3,] . . . . .
[4,] . . . . .
[5,] 0.13 . . . .print(object.size(mat_sparse),units="auto")
1.1 MbSe inspecionarmos de maneira detalhada um objeto dgCMatrix, vemos que temos três atributos importantes:
i– vetor com o índice da linha de todos os elementos não-zero.p– vetor com o índice da coluna de todos os elementos não-zero.x– vetor com os valores de todos os elementos não-zero.
str(mat_sparse)
Formal class 'dgCMatrix' [package "Matrix"] with 6 slots
..@ i : int [1:100000] 4 13 16 28 29 36 57 61 80 106 ...
..@ p : int [1:1001] 0 100 211 316 412 522 620 724 806 894 ...
..@ Dim : int [1:2] 1000 1000
..@ Dimnames:List of 2
.. ..$ : NULL
.. ..$ : NULL
..@ x : num [1:100000] 0.129 0.111 0.498 -1.138 1.254 ...
..@ factors : list()Para que {RcppArmadillo} nos retorne um objeto dgCMatrix, é simples: basta a função retornar um objeto arma::sp_mat. Este exemplo foi retirado da vinheta de Matriz Esparsa do {RcppArmadillo}.
#include <RcppArmadillo.h>
using namespace Rcpp;
using namespace arma;
// [[Rcpp::depends(RcppArmadillo)]]
// [[Rcpp::export]]
sp_mat sqrt_arma(sp_mat& X) {
return sqrt(X);
}i <- c(1,3:8)
p <- c(2,9,6:10)
x <- 7 * (1:7)
A <- sparseMatrix(i, p, x = x)
sqrt_arma(A)
8 x 10 sparse Matrix of class "dgCMatrix"
[1,] . 2.6 . . . . . . . .
[2,] . . . . . . . . . .
[3,] . . . . . . . . 3.7 .
[4,] . . . . . 4.6 . . . .
[5,] . . . . . . 5.3 . . .
[6,] . . . . . . . 5.9 . .
[7,] . . . . . . . . 6.5 .
[8,] . . . . . . . . . 7Eigen
Eigen é uma biblioteca de C++ para álgebra linear: matrizes, vetores, solucionadores numéricos e algoritmos relacionados. Ela suporta matrizes densas e esparsas em números inteiros (int), de ponto flutuante (float e double) e complexos (complex), decomposições de matrizes e soluções de sistemas lineares. Seu desempenho em muitos algoritmos é comparável a algumas das melhores implementações baseadas em LAPACK e BLAS (exemplo Armadillo).
Eigen não tem nenhuma dependência externa, apenas da biblioteca padrão C++11 STL (que todo compilador C++ dá suporte). Além disso, Eigen usa o sistema de build CMake, mas apenas para construir a documentação e os testes de unidade, e para automatizar a instalação. Se você deseja apenas usar o Eigen, pode usar os arquivos header imediatamente. Não há biblioteca binária para vincular e nenhum arquivo header configurado. Eigen é uma biblioteca pura definida nos headers.
Por conta dessa simplicidade, facilidade de instalação (virtualmente sem dependências) e alta compatibilidade, eu prefiro Eigen ao invés de Armadillo. Além disso, nos meus benchmarks quase sempre Eigen é mais rápida que Armadillo2.
Para Eigen recomendo as seguintes referências (todas do site do Eigen):
- Getting Started
- Referência Rápida de Matrizes/Vetores Densos
- Documentação das Decomposições e Soluções Lineares de Matrizes/Vetores Densos
- Referência Rápida de Matrizes/Vetores Esparsas
- Catálogo de Operações Matemáticas de Elementos de Matrizes/Vetores Densos
Classes do Eigen
Na mesma pegada do Armadillo, Eigen possui algumas categorias de classes para representar diferentes objetos de álgebra linear.
A classe Matrix lida com matrizes e vetores densos, não-esparsos. E a classe SparseMatrix lida com matrizes e vetores esparsos. Matrizes densas e vetores são arranjos comuns de elementos. Todos os elementos são armazenados em uma matriz contígua comum. Isso é diferente de matrizes e vetores esparsos, onde os elementos são armazenados como uma lista de elementos diferentes de zero.
Eigen é muito mais simples: tudo é Matrix ou SparseMatrix/SparseVector. Matrix aceita três argumentos de template (o que vai entre <>):
- tipo de escalar (ex,
double) - número de linhas (um
intouEigen::Dynamic) - número de colunas (um
intouEigen::Dynamic)
SparseMatrix e SparseVector também aceitam três argumentos de template (o que vai entre <>):
- tipo de escalar (ex,
double) - lógica de armazenamento (
ColMajorouRowMajor, o default éColMajor) - tipo de índice interno (default é
int).
Além disso Eigen tem uma síntaxe bem elegante para atalhos de matrizes. A lógica desses atalhos é a seguinte Classe-Numero_de_Elementos-Tipo_Escalar. Veja alguns exemplos abaixo:
// Matrizes Densas - Tamanho Fixo
Matrix<double, 3, 3> // Especificação Completa
Matrix3d // Atalho
// Matrizes Densas - Tamanho Dinâmico
Matrix<double, Dynamic, Dynamic> // Especificação Completa
MatrixXd // Atalho
// Matrizes Esparsas (Sem Atalhos e sem Fixo/Dinâmico)
SparseMatrix<double>
// Vetores em Eigen são apenas Matrizes 1-D
// Vetores Densos - Tamanho Fixo
Matrix<double, 3, 1> // Vetor Coluna - Especificação Completa
Matrix<double, 1, 3> // Vetor Linha - Especificação Completa
Vector3d // Vetor Coluna - Atalho
RowVector3d // Vetor Linha - Atalho
// Vetores Densos - Tamanho Dinâmico
Matrix<double, Dynamic, 1> // Vetor Coluna - Especificação Completa
Matrix<double, 1, Dynamic> // Vetor Linha - Especificação Completa
VectorXd // Vetor Coluna - Atalho
RowVectorXd // Vetor Linha - Atalho
// Vetores Esparsas (Sem Atalhos e sem Fixo/Dinâmico)
Eigen::SparseVector<double>
// Alguns exemplos extras para entender a lógica dos Atalhos
Matrix<float,Dynamic,Dynamic> = MatrixXf
Matrix<double,Dynamic,1> = VectorXd
Matrix<int,1,Dynamic> = RowVectorXi
Matrix<float,3,3> = Matrix3f
Matrix<float,4,1> = Vector4fTamanho Fixo vs Dinâmico
Internamente, uma matriz Eigen de tamanho fixo é apenas um array simples de C++ alocada na pilha (stack) e tem custo zero de tempo de execução. Em contraste, o array C++ de uma matriz Eigen de tamanho dinâmico é sempre alocada na heap e armazena seu número de linhas e colunas como variáveis de membro (member variables).
Para tamanhos grandes o suficiente, digamos, para tamanhos maiores que (aproximadamente) 32, o benefício de desempenho de usar tamanhos fixos torna-se insignificante. Pior, tentar criar uma matriz muito grande usando tamanhos fixos dentro de uma função pode resultar em um stack overflow, já que Eigen tentará alocar o array automaticamente como uma variável local, e isso normalmente é feito na pilha (stack). Finalmente, dependendo das circunstâncias, Eigen também pode ser mais agressivo tentando vetorizar (usar instruções SIMD) quando tamanhos dinâmicos são usados.
Meu conselho: use sempre matrizes e vetores de tamanho dinâmico e seja feliz sabendo que na maioria das vezes eles serão mais rápidos que os de tamanho fixo.
Acessando e Modificando Elementos
O principal meio de acessar elementos e modificar do Eigen é pelo operador (). Para matrizes use dois índices (linha, coluna) e para vetores apenas use um índice (índice). Geralmente m é uma matriz e v é um vetor.
m(0,0) = 3;
v(0) = 4;Fatiando (Slice) Matrizes e Vetores
Tem várias maneiras de fatiar (slice) matrizes e vetores. Veja alguns exemplos:
// Vetores
v.head(n)
v.tail(n)
v.segment(pos,n)
// Matriz
m.block(i,j,rows,cols)
// Matriz - Cantos (Corners)
m.topLeftCorner(rows,cols)
m.topRightCorner(rows,cols)
m.bottomLeftCorner(rows,cols)
m.bottomRightCorner(rows,cols)
m.topRows(rows)
m.bottomRows(rows)
m.leftCols(cols)
m.rightCols(cols)Inicializando Matrizes e Vetores
Por padrão os elementos de uma matriz não são inicializados na sua criação. Há algumas maneiras de inicializar os elementos de uma matriz ou vetor em Eigen:
Inicialização usando a vírgula (Comma Initialization)
Matrix3f m; // pode ser também MatrixXd m << 1, 2, 3, 4, 5, 6, 7, 8, 9;Matrizes especiais. Existem alguns métodos estáticos para todas as classes
Matrix. Eles são apenas para tamanhos fixos.// Matriz com Zeros Matrix2d::Zero() // Matrizes Aleatórias Matrix2i::Random() // Matriz Identidade Matrix3d::Identity() // Vetores Espaçados Linearmente (size, low, high) // tipo um seq() do R VectorXf v; v.setLinSpaced(5,0.5f,1.5f);
Tamanho e Dimensões
O tamanho atual de uma matriz pode ser recuperado por .rows(), .cols() e .size(). Esses métodos retornam o número de linhas, o número de colunas e o número de elementos, respectivamente. O redimensionamento de uma matriz de tamanho dinâmico é feito pelo método .resize().
m.cols();
m.rows();
m.resize(4,4);Operações Aritméticas com Matrizes e Vetores
Todos os vetores e matrizes de Eigen aceitam adição, subtração, multiplicação, divisão: +,-, *, /. Além disso, tem MUITAS outras operações e decomposições que podem ser feitas. Não vou listar todas aqui, consulte a documentação do Eigen.
Como usar Eigen com {Rcpp} – {RcppEigen}
Primeiro, certifique-se que você possui a biblioteca Eigen instalada:
- Linux:
sudo apt install libeigen3-dev - MacOS:
brew install eigen - Windows: baixe no site do
Eigen
Segundo, installe o pacote {RcppEigen} para R.
Terceiro, coloque em todo código que deseja usar o Eigen com {Rcpp} a seguinte síntaxe:
#include <RcppEigen.h>
using namespace Eigen;
// [[Rcpp::depends(RcppEigen)]]Atenção!: não usar o header do {Rcpp} (#include <Rcpp.h>), pois ele conflita com o header do {RcppEigen} (#include <RcppEigen.h>).
Pronto! É isso.
Conversões do {RcppEigen}
O {RcppEigen} automaticamente converterá os tipos de retorno das funções na seguinte lógica:
| Tipo de Objeto R | Classe Eigen |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Como usar Matrizes Esparsas no {RcppEigen}
Para que {RcppEigen} nos retorne um objeto dgCMatrix, é simples: basta a função retornar um objeto Eigen::SparseMatrix<double>. Vou usar o mesmo exemplo de operação com matriz esparsa do {RcppArmadillo}:
#include <RcppEigen.h>
using namespace Rcpp;
using namespace Eigen;
// [[Rcpp::depends(RcppEigen)]]
// [[Rcpp::export]]
SparseMatrix<double> sqrt_eigen(SparseMatrix<double>& X) {
return X.cwiseSqrt();
}i <- c(1,3:8)
p <- c(2,9,6:10)
x <- 7 * (1:7)
A <- sparseMatrix(i, p, x = x)
sqrt_eigen(A)
8 x 10 sparse Matrix of class "dgCMatrix"
[1,] . 2.6 . . . . . . . .
[2,] . . . . . . . . . .
[3,] . . . . . . . . 3.7 .
[4,] . . . . . 4.6 . . . .
[5,] . . . . . . 5.3 . . .
[6,] . . . . . . . 5.9 . .
[7,] . . . . . . . . 6.5 .
[8,] . . . . . . . . . 7Benchmarks
Está na hora de mais uma vez colocarmos o que vimos em prática. Além disso fazer alguns benchmarks de Eigen vs Armadillo.
Exemplo – Multiplicação de Matrizes
Nesse caso vamos comparar multiplicar duas matrizes em C++ usando o {Rcpp}, {RcppArmadillo} e {RcppEigen}
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector mat_mul(const NumericVector& A, const NumericVector& B) {
NumericVector C = A * B;
// dimensões para Vector virar Matrix no R
int dim = sqrt(A.length());
C.attr("dim") = Dimension(dim, dim);
return C;
}#include <RcppArmadillo.h>
using namespace Rcpp;
using namespace arma;
// [[Rcpp::depends(RcppArmadillo)]]
// [[Rcpp::export]]
mat mat_mul_arma(const mat& A, const mat& B) {
return A * B;
}#include <RcppEigen.h>
using namespace Rcpp;
using namespace Eigen;
// [[Rcpp::depends(RcppEigen)]]
// [[Rcpp::export]]
MatrixXd mat_mul_eigen(const MatrixXd& A, const MatrixXd& B){
return A * B;
}b1 <- bench::press(
n = 10^c(1:3),
{
X = matrix(rnorm(n * n), nrow = n)
bench::mark(
Rcpp = mat_mul(X, X),
arma = mat_mul_arma(X, X),
eigen = mat_mul_eigen(X, X),
check = FALSE,
relative = TRUE
)
})
b1
# A tibble: 9 x 7
expression n min median `itr/sec` mem_alloc `gc/sec`
<bch:expr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Rcpp 10 1 1 1.09 1 2.17
2 arma 10 1.37 1.20 1 1 1
3 eigen 10 1.28 1.12 1.08 1 1.08
4 Rcpp 100 1 1 69.5 1 87.7
5 arma 100 71.9 71.6 1 1 1
6 eigen 100 19.4 18.9 3.61 1 4.69
7 Rcpp 1000 1 1 223. 1 Inf
8 arma 1000 585. 222. 1 1 NaN
9 eigen 1000 134. 51.2 4.31 1 NaN 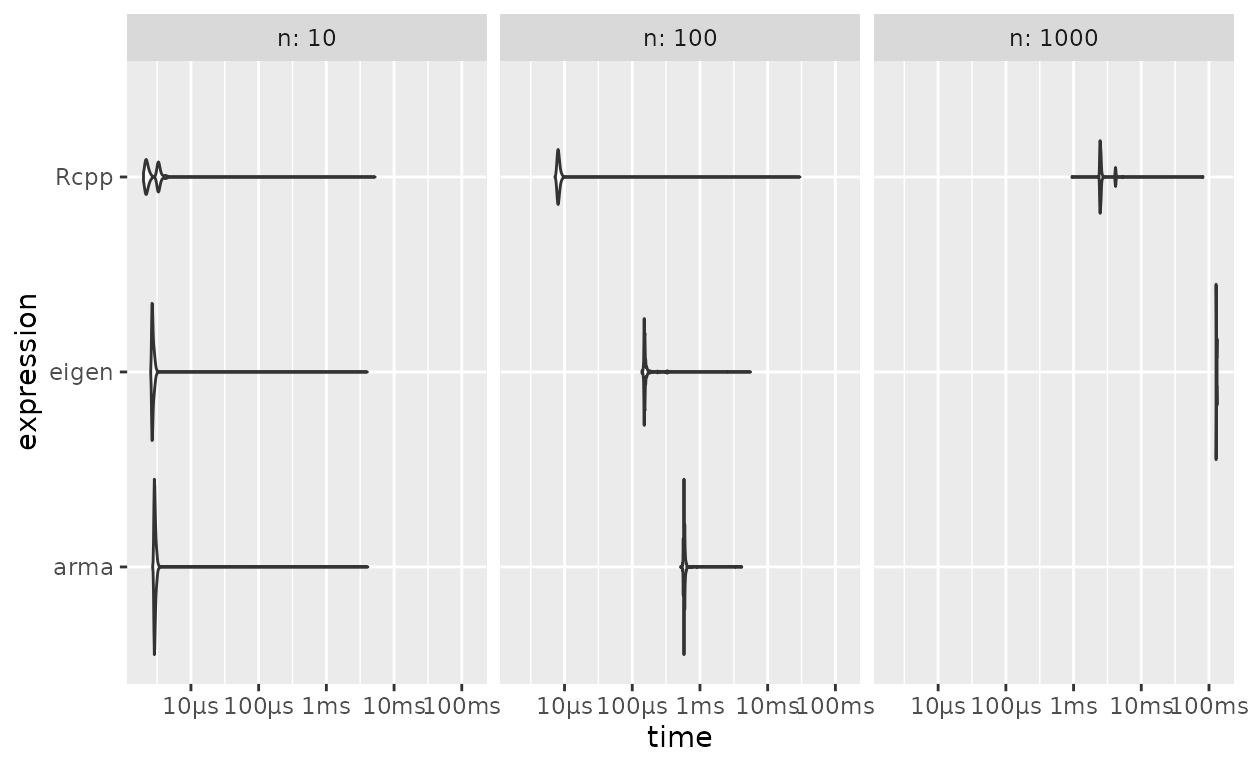
Figure 2: Benchmarks de Multiplicação de Matriz: Rcpp vs Armadillo vs Eigen
No meu computador {RcppEigen} é mais rápido que {RcppArmadillo}, mas ambos são mais lentos que uma implementação simples com {Rcpp}.
Exemplo – Matriz Esparsa
Vamos usar mat_sparse criada que possui dimensão 1.000 x 1.000 e tomar a raiz quadrada de todos os elementos.
b2 <- bench::mark(
arma = sqrt_eigen(mat_sparse),
eigen = sqrt_eigen(mat_sparse),
relative = TRUE
)
b2
# A tibble: 2 x 6
expression min median `itr/sec` mem_alloc `gc/sec`
<bch:expr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 arma 1 1.00 1 1.00 1
2 eigen 1.02 1 1.08 1 1.08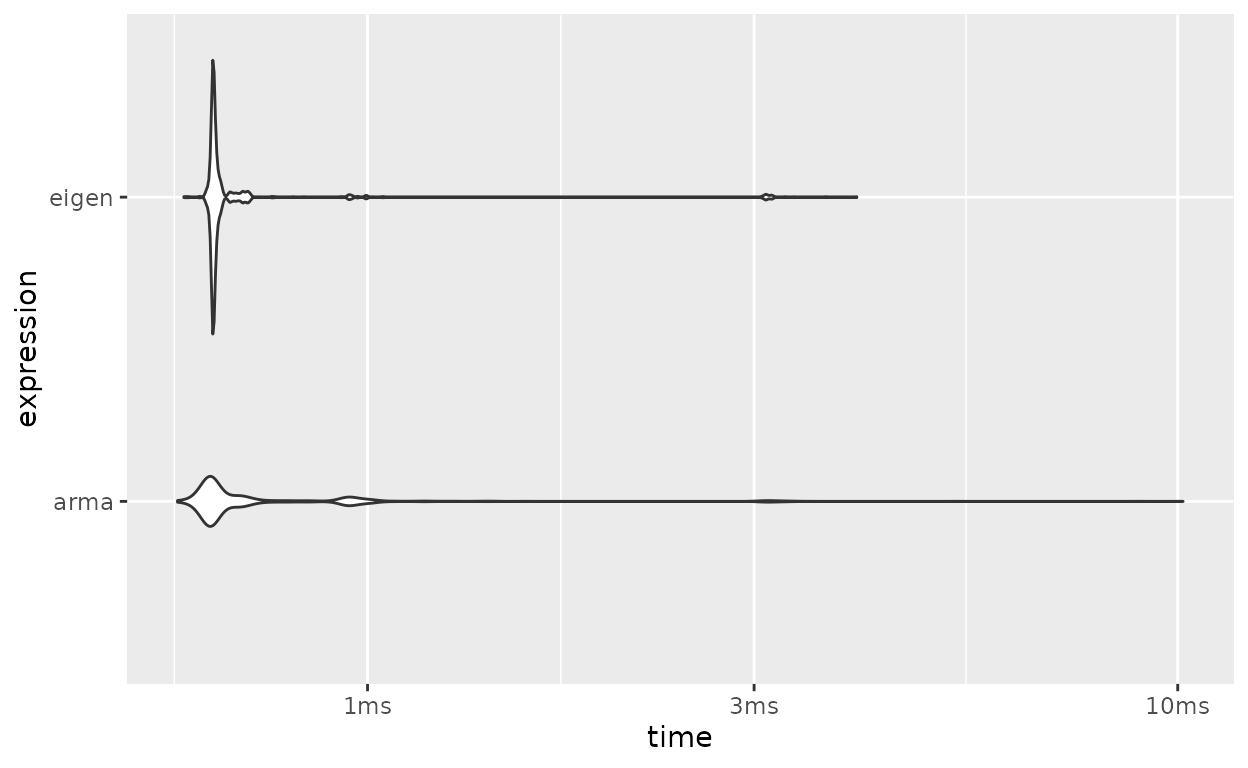
Figure 3: Benchmarks de Matriz Esparsa: Armadillo vs Eigen
Novamente Eigen é um pouco mais rápida que Armadillo, mas a diferença é pequena.
Exemplo – Regressão Linear fast_lm()
Esse exemplo, originalmente do criador dos pacotes do ecossistema {Rcpp} Dirk Eddelbuettel na vinheta introdutória do {Rcpp}, é bem interessante. Aqui vamos aplicar uma regressão linear tanto em Armadillo quando em Eigen. Ambos usam o solve() que é um solucionador de sistemas de equações lineares3.
#include <RcppArmadillo.h>
using namespace arma;
// [[Rcpp::depends(RcppArmadillo)]]
// [[Rcpp::export]]
Rcpp::List fast_lm_arma(const vec& y, const mat& X) {
int n = X.n_rows, k = X.n_cols;
colvec coef = solve(X, y);
colvec resid = y - X*coef;
double sig2 = as_scalar(trans(resid)*resid/(n-k));
colvec stderrest = sqrt(sig2 * diagvec(inv(trans(X)*X)));
return Rcpp::List::create(Rcpp::Named("coefficients") = coef,
Rcpp::Named("stderr") = stderrest);
}#include <RcppEigen.h>
using namespace Eigen;
// [[Rcpp::depends(RcppEigen)]]
// [[Rcpp::export]]
Rcpp::List fast_lm_eigen(const VectorXd& y, const MatrixXd& X) {
int n = X.rows(), k = X.cols();
// Usando SVD Decomposition
//VectorXd coef = X.bdcSvd(ComputeThinU | ComputeThinV).solve(y);
// Usando QR Decomposition
//VectorXd coef = X.colPivHouseholderQr().solve(y);
// Usando Normal Equations com LDL Decomposition (mais rápida)
VectorXd coef = (X.transpose() * X).ldlt().solve(X.transpose() * y);
VectorXd resid = y - X*coef;
double sig2 = resid.squaredNorm() / (n - k);
VectorXd stderrest = (sig2 * ((X.transpose() * X).inverse()).diagonal()).array().cwiseSqrt();
return Rcpp::List::create(Rcpp::Named("coefficients") = coef,
Rcpp::Named("stderr") = stderrest);
}y <- log(trees$Volume)
X <- cbind(1, log(trees$Girth))
b3 <- bench::mark(
R = lm(y ~ X),
arma = fast_lm_arma(y, X),
eigen = fast_lm_eigen(y, X),
check = FALSE,
relative = TRUE
)
b3
# A tibble: 3 x 6
expression min median `itr/sec` mem_alloc `gc/sec`
<bch:expr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 R 117. 114. 1 191. Inf
2 arma 1.50 1.40 72.2 1 NaN
3 eigen 1 1 109. 1 Inf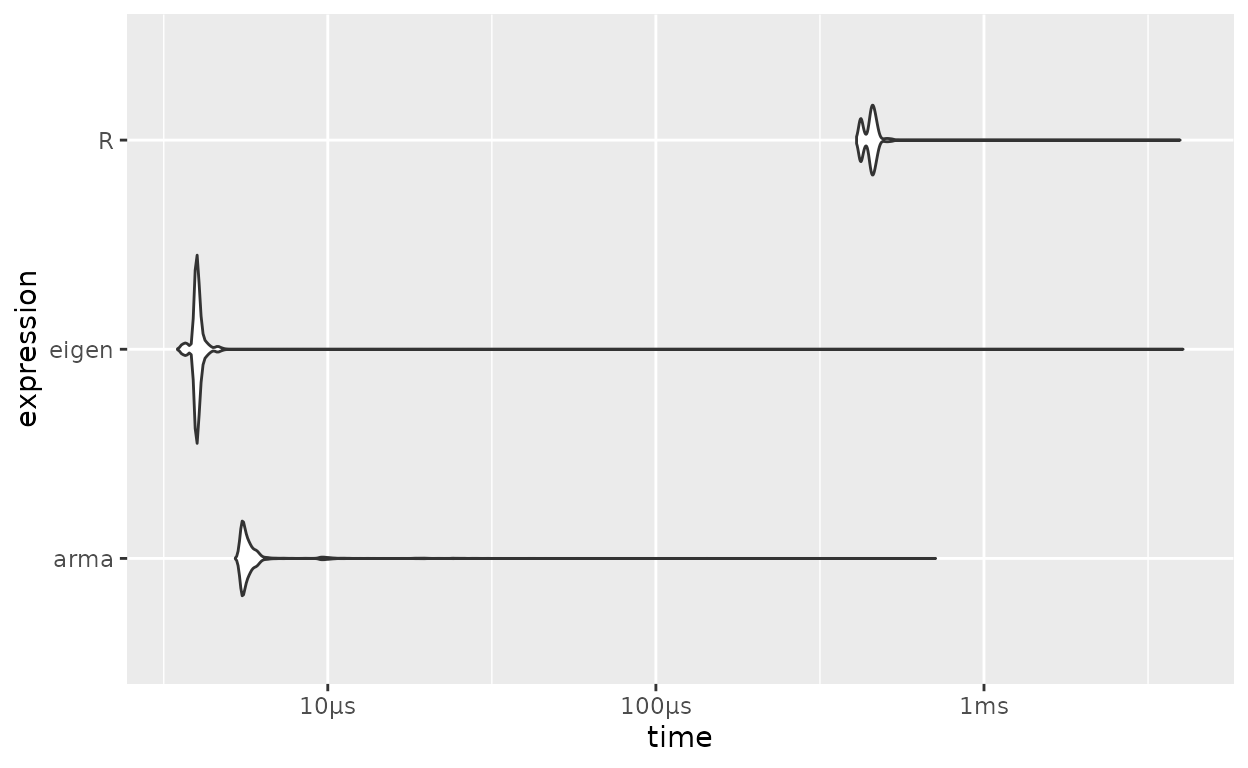
Figure 4: Benchmarks de Regressão Linear: R vs Armadillo vs Eigen
Tanto Eigen quanto Armadillo são rápidos! Quase 100x mais rápidos 🤯. Novamente a diferença entre Eigen e Armadillo é pequena.
Usar {RcppArmadillo} ou {RcppEigen} no seu Pacote R
Eu recomendo usar o pacote {usethis} e seguir as instruções.
Ambiente
R version 4.0.4 (2021-02-15)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 20.10
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] dplyr_1.0.5 gt_0.2.2 Matrix_1.3-2
loaded via a namespace (and not attached):
[1] RcppEigen_0.3.3.9.1 tidyselect_1.1.0
[3] xfun_0.22 bslib_0.2.4
[5] purrr_0.3.4 lattice_0.20-41
[7] colorspace_2.0-0 vctrs_0.3.6
[9] generics_0.1.0 htmltools_0.5.1.1
[11] emo_0.0.0.9000 yaml_2.2.1
[13] utf8_1.1.4 rlang_0.4.10
[15] jquerylib_0.1.3 pillar_1.5.1
[17] glue_1.4.2 DBI_1.1.1
[19] jpeg_0.1-8.1 lifecycle_1.0.0
[21] stringr_1.4.0 munsell_0.5.0
[23] commonmark_1.7 gtable_0.3.0
[25] ragg_1.1.1 bench_1.1.1
[27] evaluate_0.14 knitr_1.31
[29] RcppArmadillo_0.10.2.2.0 parallel_4.0.4
[31] fansi_0.4.2 profmem_0.6.0
[33] highr_0.8 Rcpp_1.0.6
[35] scales_1.1.1 backports_1.2.1
[37] checkmate_2.0.0 jsonlite_1.7.2
[39] debugme_1.1.0 farver_2.1.0
[41] systemfonts_1.0.1 textshaping_0.3.2
[43] distill_1.2 ggplot2_3.3.3
[45] digest_0.6.27 stringi_1.5.3
[47] grid_4.0.4 cli_2.3.1
[49] tools_4.0.4 magrittr_2.0.1
[51] sass_0.3.1 tibble_3.1.0
[53] tidyr_1.1.3 crayon_1.4.1
[55] pkgconfig_2.0.3 downlit_0.2.1
[57] ellipsis_0.3.1 lubridate_1.7.10
[59] rstudioapi_0.13 assertthat_0.2.1
[61] rmarkdown_2.7 R6_2.5.0
[63] compiler_4.0.4