Estatística Bayesiana com R e Stan: Distribuições Estatísticas

Jose Storopoli

Processing math: 100%

Distribuições Estatísticas

Os blocos fundamentais dos modelos Bayesianos

Author

Affiliation

Jose Storopoli

UNINOVE

Published

Aug. 1, 2021

Citation

Storopoli, 2021

A estatística Bayesiana usa distribuições probabilísticas como o motor de sua inferência na elaboração dos valores dos parâmetros estimados e suas incertezas.

Imagine que distribuição probabilísticas são pequenas peças de “Lego.” Podemos construir o que quisermos com essas pequenas peças. Podemos fazer um castelo, uma casa, uma cidade; literalmente o que quisermos. O mesmo é valido para modelos probabilísticos em estatística Bayesiana. Podemos construir modelos dos mais simples aos mais complexo a partir de distribuições probabilísticas e suas relações entre si. Nesta aula vamos fazer um sobrevoo sobre as principais distribuições probabilísticas, sua notação matemática e seus principais usos em estatística Bayesiana.

Uma distribuição de probabilidade é a função matemática que fornece as probabilidades de ocorrência de diferentes resultados possíveis para um experimento. É uma descrição matemática de um fenômeno aleatório em termos de seu espaço amostral e as probabilidades de eventos (subconjuntos do espaço amostral).

Geralmente usamos a notação X ~ Dist(par1, par2, ...). Onde X é a variável, Dist é o nome da distribuição, e par os parâmetros que definem como a distribuição se comporta. Toda distribuição probabilística pode ser “parameterizada” ao especificarmos parâmetros que permitem moldarmos alguns aspectos da distribuição para algum fim específico.

Começaremos pelas distribuições discretas e na sequência abordaremos as contínuas.

Discretas

Distribuições de probabilidade discretas são aquelas que os resultados são números discretos (também chamados de números inteiros): $-N, \dots, -2, 1, 0,1,2,\dots, N$ e $N \in \mathbb{Z}$ . Em distribuições discretas chamamos a probabilidade de uma distribuição tomar certos valores como “massa.” A função massa de probabilidade $\text{FMP}$ é a função que especifica a probabilidade da variável aleatória $X$ tomar o valor $x$ :

$\text{FMP}(x) = P(X = x)$

Uniforme Discreta

A distribuição uniforme discreta é uma distribuição de probabilidade simétrica em que um número finito de valores são igualmente prováveis de serem observados. Cada um dos $n$ valores tem probabilidade igual $\frac{1}{n}$ . Outra maneira de dizer “distribuição uniforme discreta” seria “um número conhecido e finito de resultados igualmente prováveis de acontecer.”

A distribuição uniforme discreta possui dois parâmetros e sua notação é $\text{Unif}(a, b)$ :

Limite Inferior ( $a$ )
Limite Superior ( $b$ )

Exemplo: Um dado.

ggplot(data = tibble(
  x = seq(1, 6),
  y = dunif(x, min = 1, max = 6)),
  aes(x, y)) +
  geom_line(size = 2, col = "red") +
  geom_point(size = 4, col = "red") +
  labs(
    title = "Distribuição Uniforme Discreta",
    subtitle = expression("a =  1, b = 6"),
    x = expression(theta),
    y = "Massa",
    color = "Parâmetros"
  ) +
  scale_x_continuous(breaks = c(1:6))

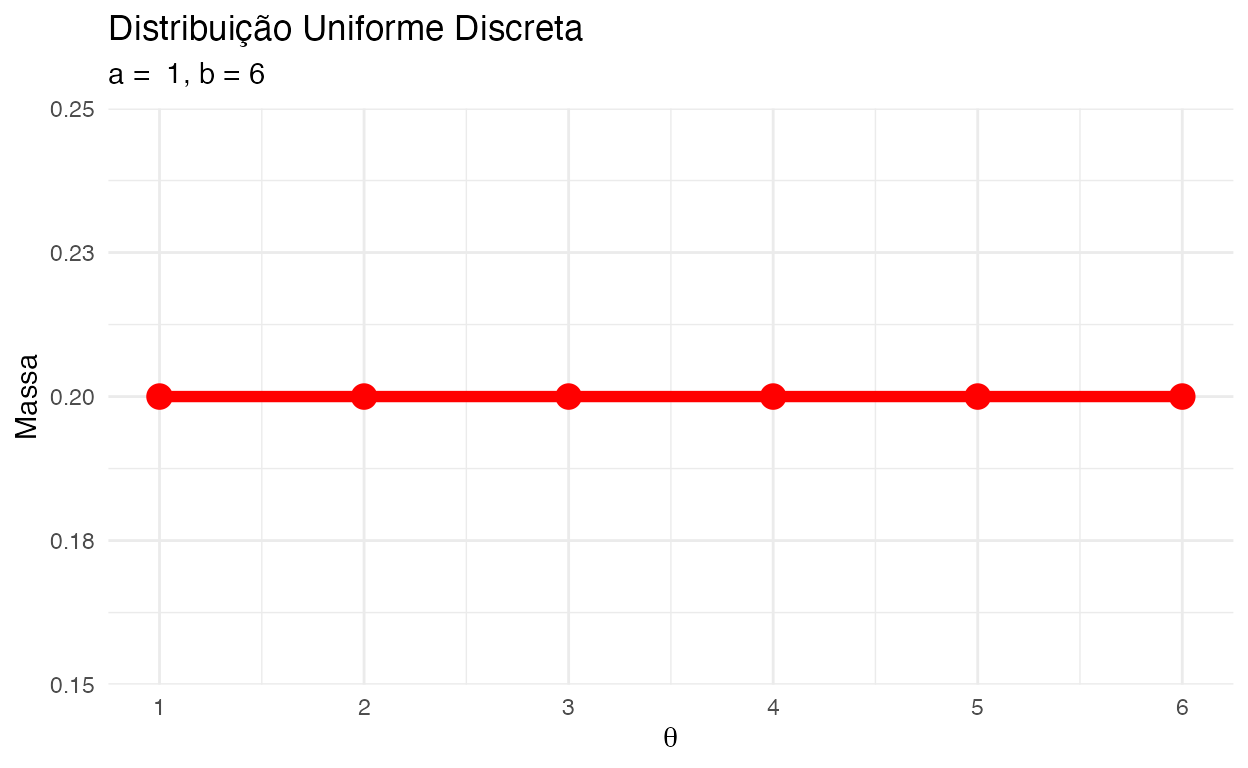
Figure 1: Distribuição Uniforme entre 1 e 6

Bernoulli

A distribuição de Bernoulli descreve um evento binário de um sucesso de um experimento. Geralmente representamos $0$ como falha e $1$ como sucesso, então o resultado de uma distribuição de Bernoulli é uma variável binária $Y \in \{0, 1\}$ .

A distribuição de Bernoulli é muito usada para modelar resultados discretos binários no qual só há dois possíveis resultados.

A distribuição de Bernoulli possui apenas um único paramêtro e sua notação é $\text{Bernoulli} (p)$ :

Probabilidade de Sucesso ( $p$ )

Exemplo: Se o paciente sobreviveu ou morreu ou se o cliente conclui sua compra ou não.

Binomial

A distribuição binomial descreve um evento do número de sucessos em uma sequência de $n$ experimentos independentes, cada um fazendo uma pergunta sim-não com probabilidade de sucesso $p$ . Note que a distribuição de Bernoulli é um caso especial da distribuição binomial no qual o número de experimentos é $1$ .

A distribuição binomial possui dois parâmetros e sua notação é $\text{Bin}(n, p)$ ou $\text{Binomial}(n, p)$ :

Número de Experimentos ( $n$ )
Probabilidade de Sucessos ( $p$ )

Exemplo: quantidade de caras em 5 lançamentos de uma moeda.

ggplot(data = tibble(x = seq(0, 5))) +
  labs(
    title = "Comparativo de Distribuições Binomial",
    subtitle = expression(n == 5),
    x = expression(theta),
    y = "Massa",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dbinom(x, size = 5, prob = 0.1), color = "p ==  0.1"), size = 2) +
  geom_point(aes(x, y = dbinom(x, size = 5, prob = 0.1), color = "p ==  0.1"), size = 4) +
  geom_line(aes(x, y = dbinom(x, size = 5, prob = 0.2), color = "p ==  0.2"), size = 2) +
  geom_point(aes(x, y = dbinom(x, size = 5, prob = 0.2), color = "p ==  0.2"), size = 4) +
  geom_line(aes(x, y = dbinom(x, size = 5, prob = 0.5), color = "p ==  0.5"), size = 2) +
  geom_point(aes(x, y = dbinom(x, size = 5, prob = 0.5), color = "p ==  0.5"), size = 4) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

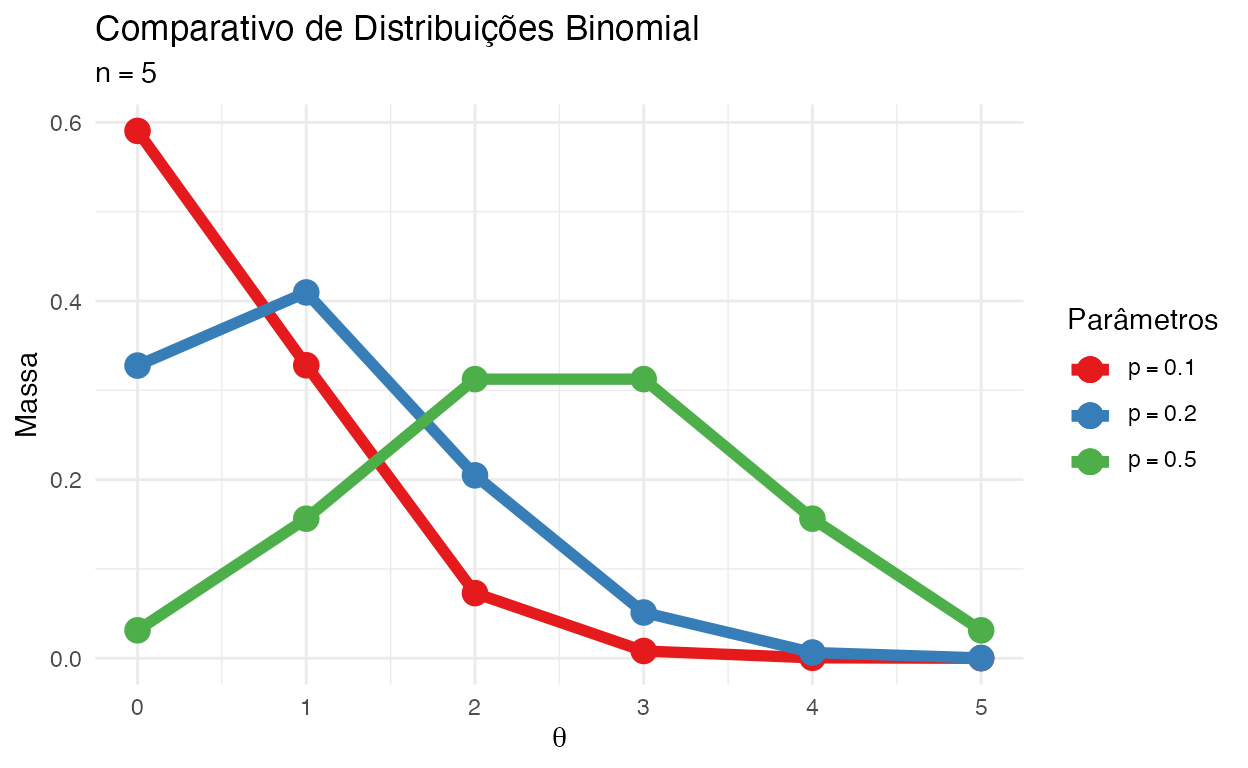
Figure 2: Comparativo de Distribuições Binomial

Poisson

A distribuição Poisson expressa a probabilidade de um determinado número de eventos ocorrerem em um intervalo fixo de tempo ou espaço se esses eventos ocorrerem com uma taxa média constante conhecida e independentemente do tempo desde o último evento. A distribuição de Poisson também pode ser usada para o número de eventos em outros intervalos especificados, como distância, área ou volume.

A distribuição Poisson possui um parâmetro e sua notação é $\text{Poisson}(\lambda)$ :

Taxa ( $\lambda$ )

Exemplo: Quantidade de e-mails que você recebe diariamente. Quantidade de buracos que você encontra na rua.

ggplot(data = tibble(x = seq(0, 20))) +
  labs(
    title = "Comparativo de Distribuições Poisson",
    x = expression(theta),
    y = "Massa",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dpois(x, lambda = 1), color = "lambda ==  1"), size = 2) +
  geom_point(aes(x, y = dpois(x, lambda = 1), color = "lambda ==  1"), size = 4) +
  geom_line(aes(x, y = dpois(x, lambda = 4), color = "lambda ==  4"), size = 2) +
  geom_point(aes(x, y = dpois(x, lambda = 4), color = "lambda ==  4"), size = 4) +
  geom_line(aes(x, y = dpois(x, lambda = 10), color = "lambda ==  10"), size = 2) +
  geom_point(aes(x, y = dpois(x, lambda = 10), color = "lambda ==  10"), size = 4) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

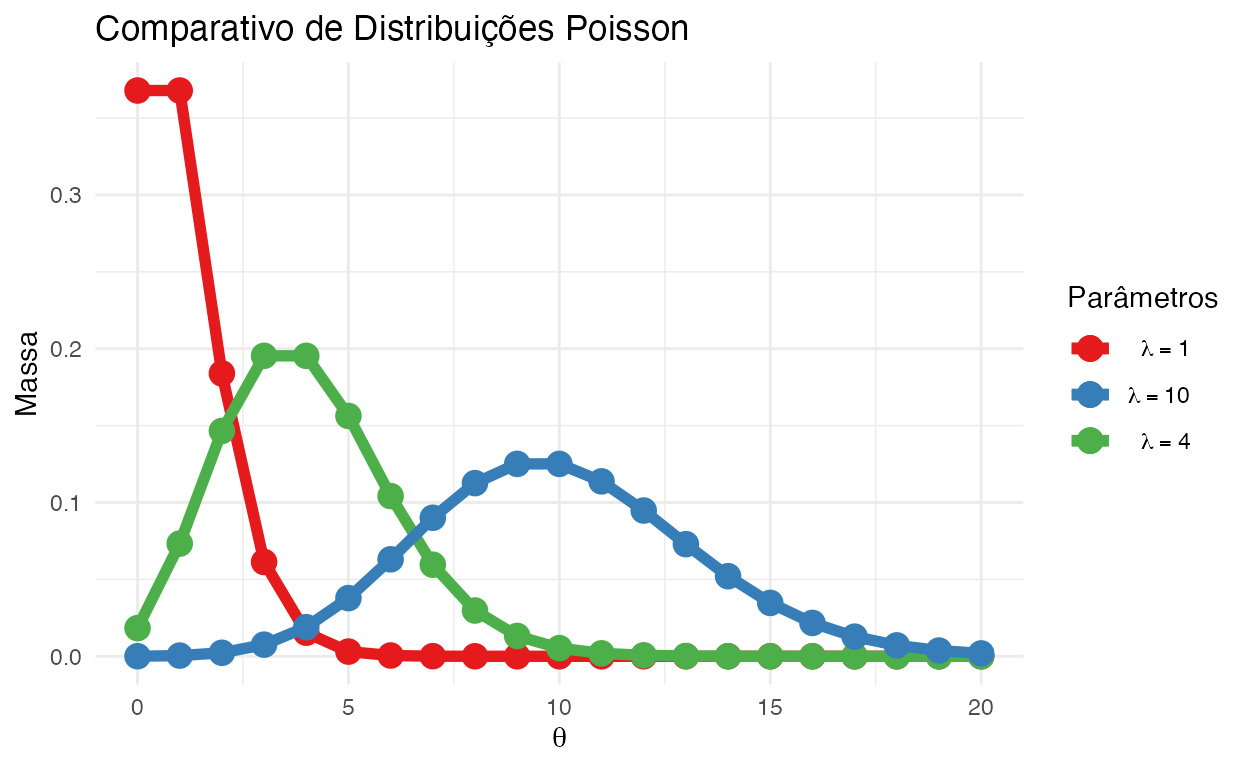
Figure 3: Comparativo de Distribuições Poisson

Binomial Negativa

A distribuição binomial negativa descreve um evento do número de sucessos em uma sequência de $n$ experimentos independentes, cada um fazendo uma pergunta sim-não com probabilidade $p$ até que se obtenha $k$ sucessos. Note que ela se torna idêntica à distribuição de Poisson quando no limite de $k \to \infty$ . Isto faz com que seja uma opção robusta para substituir uma distribuição de Poisson para modelar fenômenos com uma superdispersão (variação nos dados excedente ao esperado).

A distribuição negativa binomial possui dois parâmetros e sua notação é $\text{NB}(k, p)$ ou $\text{Negative-Binomial}(k, p)$ :

Número de Sucessos ( $k$ )
Probabilidade de Sucessos ( $p$ )

Qualquer fenômeno que pode ser modelo com uma distribuição de Poisson, pode ser modelo com uma distribuição binomial negativa (Gelman et al., 2013; Gelman, Hill, & Vehtari, 2020).

Exemplo: Contagem anual de ciclones tropicais.

ggplot(data = tibble(x = seq(0, 5))) +
  labs(
    title = "Comparativo de Distribuições Binomial Negativa",
    subtitle = expression(p == 0.5),
    x = expression(theta),
    y = "Massa",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dnbinom(x, size = 1, prob = 0.5), color = "k ==  1"), size = 2) +
  geom_point(aes(x, y = dnbinom(x, size = 1, prob = 0.5), color = "k ==  1"), size = 4) +
  geom_line(aes(x, y = dnbinom(x, size = 2, prob = 0.5), color = "k ==  2"), size = 2) +
  geom_point(aes(x, y = dnbinom(x, size = 2, prob = 0.5), color = "k ==  2"), size = 4) +
  geom_line(aes(x, y = dnbinom(x, size = 5, prob = 0.5), color = "k ==  5"), size = 2) +
  geom_point(aes(x, y = dnbinom(x, size = 5, prob = 0.5), color = "k ==  5"), size = 4) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

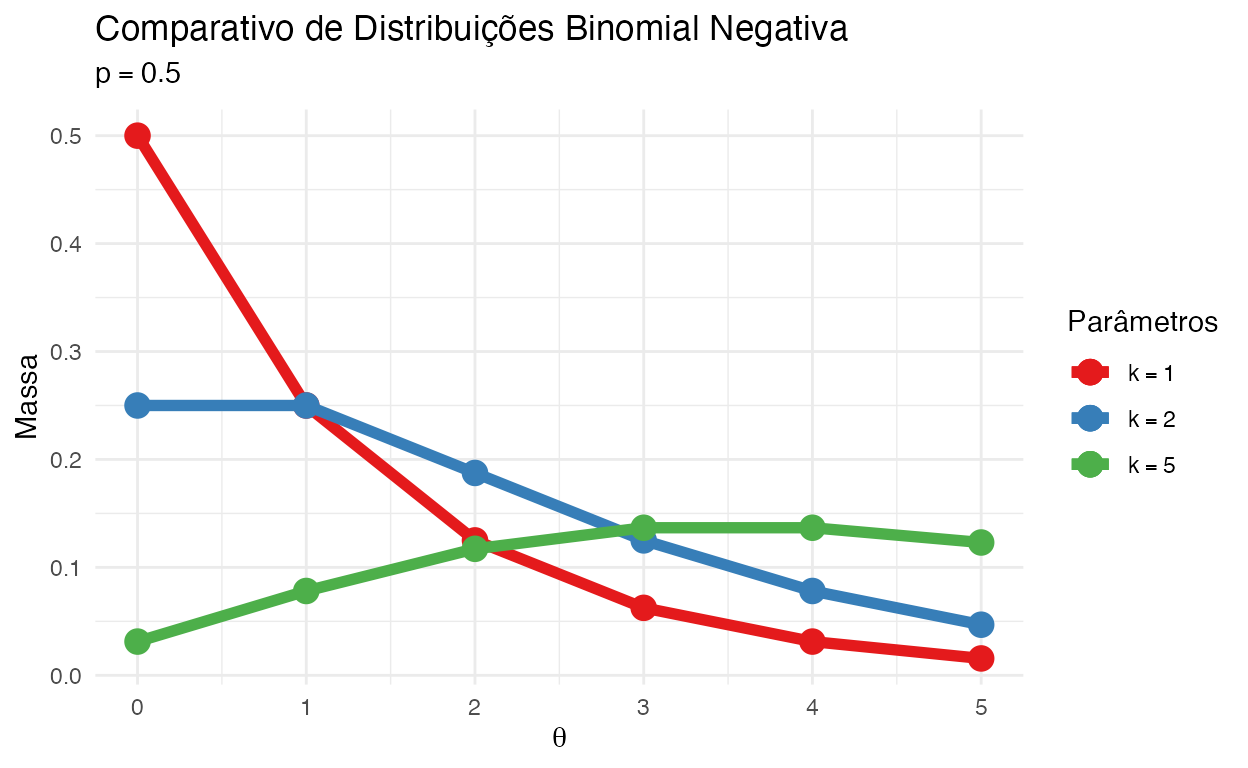
Figure 4: Comparativo de Distribuições Binomial Negativa

Contínuas

Distribuições de probabilidade contínuas são aquelas que os resultados são valores em uma faixa contínua (também chamados de número reais): $(-\infty, +\infty) \in \mathbb{R}$ . Em distribuições contínuas chamamos a probabilidade de uma distribuição tomar certos valores como “densidade.” Como estamos falando sobre números reais não conseguimos obter a probabilidade de uma variável aleatória $X$ tomar o valor de $x$ . Isto sempre será $0$ , pois não há como especificar um valor exato de $x$ . $x$ vive na linha dos números reais, portanto, precisamos especificar a probabilidade de $X$ tomar valores em um intervalo $[a,b]$ . A função densidade de probabilidade $\text{FDP}$ é definida como:

$\text{FDP}(x) = P(a \leq X \leq b) = \int_a^b f(x) dx$

Normal / Gaussiana

Essa distribuição geralmente é usada nas ciências sociais e naturais para representar variáveis contínuas na qual as suas distribuições não são conhecidas. Esse pressuposto é por conta do teorema do limite central. O teorema do limite central afirma que, em algumas condições, a média de muitas amostras (observações) de uma variável aleatória com média e variância finitas é ela própria uma variável aleatória cuja distribuição converge para uma distribuição normal à medida que o número de amostras aumenta. Portanto, as quantidades físicas que se espera sejam a soma de muitos processos independentes (como erros de medição) muitas vezes têm distribuições que são quase normais.

A distribuição normal possui dois parâmetros e sua notação é $\text{Normal}(\mu, \sigma^2)$ ou $\text{N}(\mu, \sigma^2)$ :

Média ( $\mu$ ): média da distribuição e também a moda e a mediana
Desvio Padrão ( $\sigma$ ): a variância da distribuição ( $\sigma^2$ ) é uma medida de dispersão das observações em relação à média

Exemplo: Altura, Peso etc.

ggplot(data = tibble(x = seq(-4, 4, length = 100))) +
  labs(
    title = "Comparativo de Distribuições Normais",
    subtitle = expression(mu == 0),
    x = expression(theta),
    y = "Densidade",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 0.5), color = "sigma ==  0.5"), size = 2) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 1), color = "sigma ==  1.0"), size = 2) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 2), color = "sigma ==  2.0"), size = 2) +
  geom_line(aes(x, y = dnorm(x, mean = 0, sd = 5), color = "sigma ==  5.0"), size = 2) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

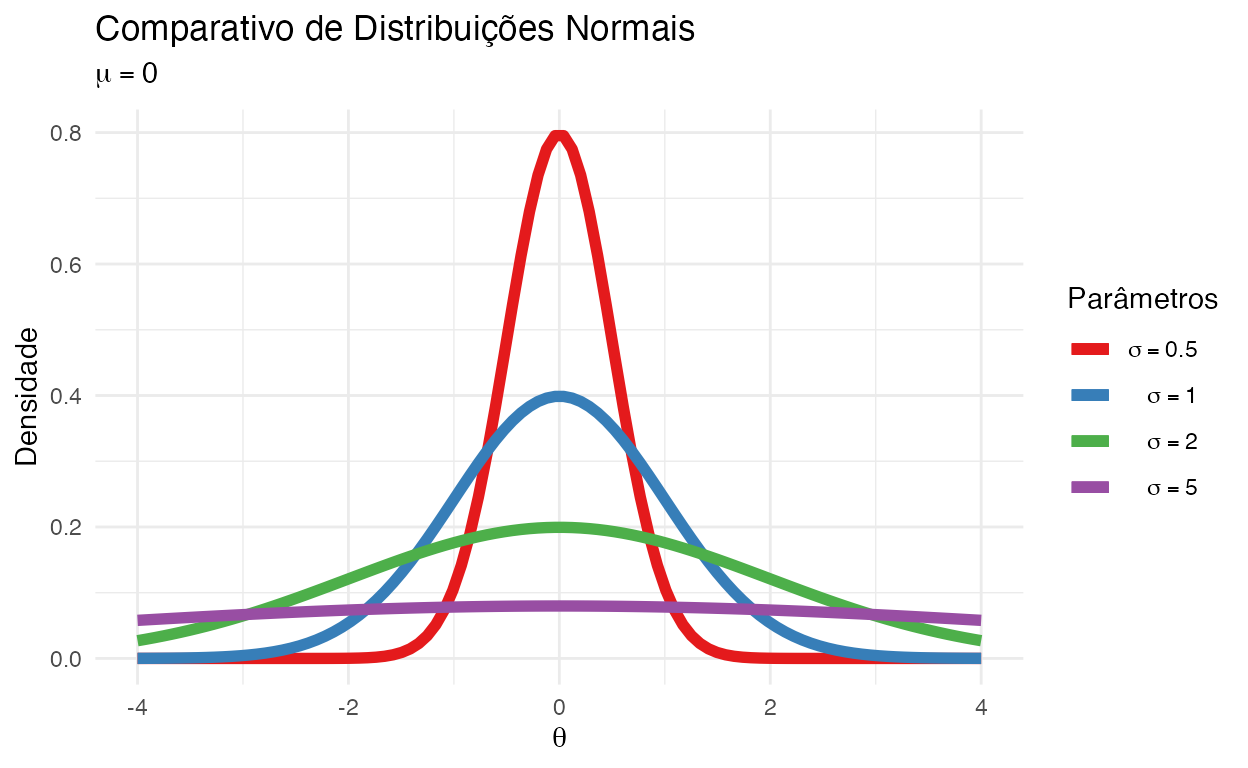
Figure 5: Comparativo de Distribuições Normais

Log-normal

A distribuição Log-normal é uma distribuição de probabilidade contínua de uma variável aleatória cujo logaritmo é normalmente distribuído. Assim, se a variável aleatória $X$ for distribuída normalmente por log natural, então $Y = \log (X)$ terá uma distribuição normal.

Uma variável aleatória com distribuição logarítmica aceita apenas valores reais positivos. É um modelo conveniente e útil para medições em ciências exatas e de engenharia, bem como medicina, economia e outros campos, por ex. para energias, concentrações, comprimentos, retornos financeiros e outros valores.

Um processo log-normal é a realização estatística do produto multiplicativo de muitas variáveis aleatórias independentes, cada uma das quais positiva.

A distribuição log-normal possui dois parâmetros e sua notação é $\text{Log-Normal}(\mu, \sigma^2)$ :

Média ( $\mu$ ): média do logaritmo natural da distribuição
Desvio Padrão ( $\sigma$ ): a variância do logaritmo natural da distribuição ( $\sigma^2$ ) é uma medida de dispersão das observações em relação à média

ggplot(data = tibble(x = seq(0, 3, length = 100))) +
  labs(
    title = "Comparativo de Distribuições Log-Normais",
    subtitle = expression(mu == 0),
    x = expression(theta),
    y = "Densidade",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dlnorm(x, mean = 0, sd = 0.25), color = "sigma ==  0.25"), size = 2) +
  geom_line(aes(x, y = dlnorm(x, mean = 0, sd = 0.5), color = "sigma ==  0.5"), size = 2) +
  geom_line(aes(x, y = dlnorm(x, mean = 0, sd = 1.0), color = "sigma ==  1.0"), size = 2) +
  geom_line(aes(x, y = dlnorm(x, mean = 0, sd = 1.5), color = "sigma ==  1.5"), size = 2) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

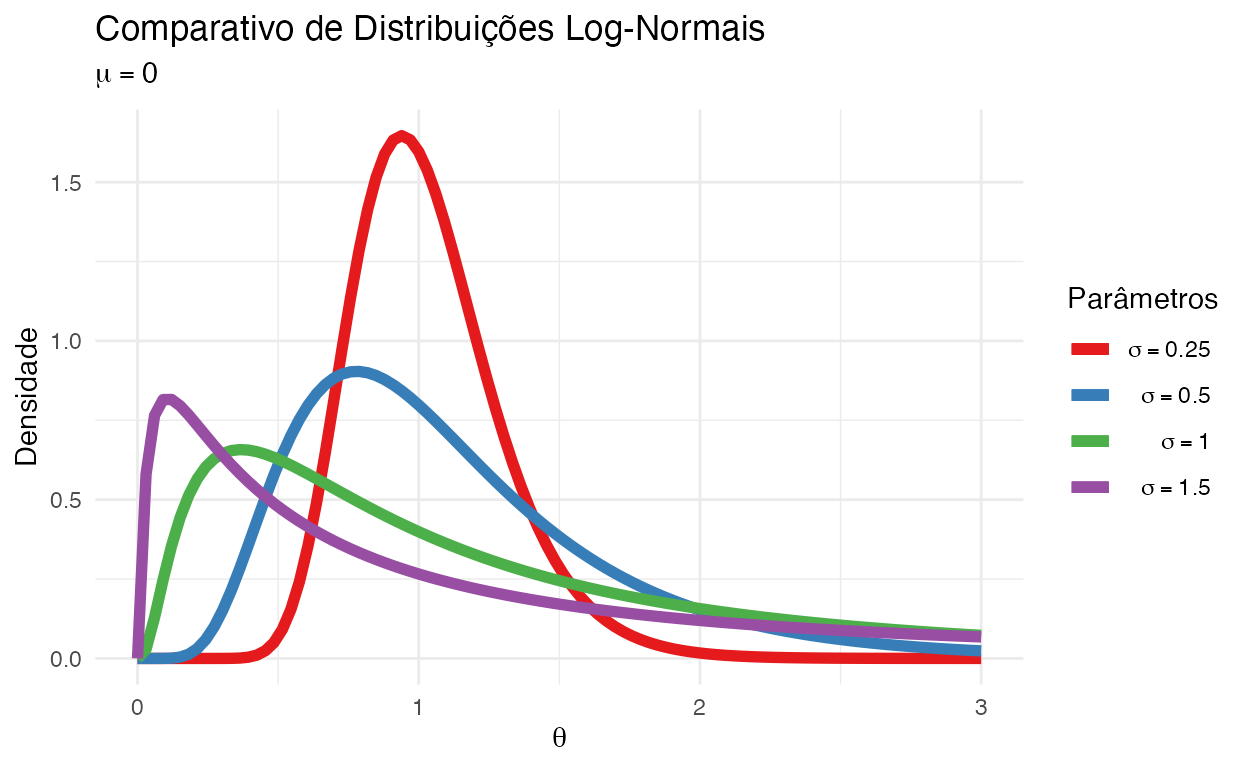
Figure 6: Comparativo de Distribuições Log-Normais

Exponencial

A distribuição exponencial é a distribuição de probabilidade do tempo entre eventos que ocorrem de forma contínua e independente a uma taxa média constante.

A distribuição exponencial possui um parâmetro e sua notação é $\text{Exp}(\lambda)$ :

Taxa ( $\lambda$ )

Exemplo: Quanto tempo até o próximo terremoto. Quanto tempo até o próximo ônibus.

ggplot(data = tibble(x = seq(0, 5, length = 100))) +
  labs(
    title = "Comparativo de Distribuições Exponenciais",
    x = expression(theta),
    y = "Densidade",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dexp(x, rate = 0.5), color = "lambda ==  0.5"), size = 2) +
  geom_line(aes(x, y = dexp(x, rate = 1), color = "lambda ==  1"), size = 2) +
  geom_line(aes(x, y = dexp(x, rate = 1.5), color = "lambda ==  1.5"), size = 2) +
  geom_line(aes(x, y = dexp(x, rate = 2), color = "lambda ==  2"), size = 2) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

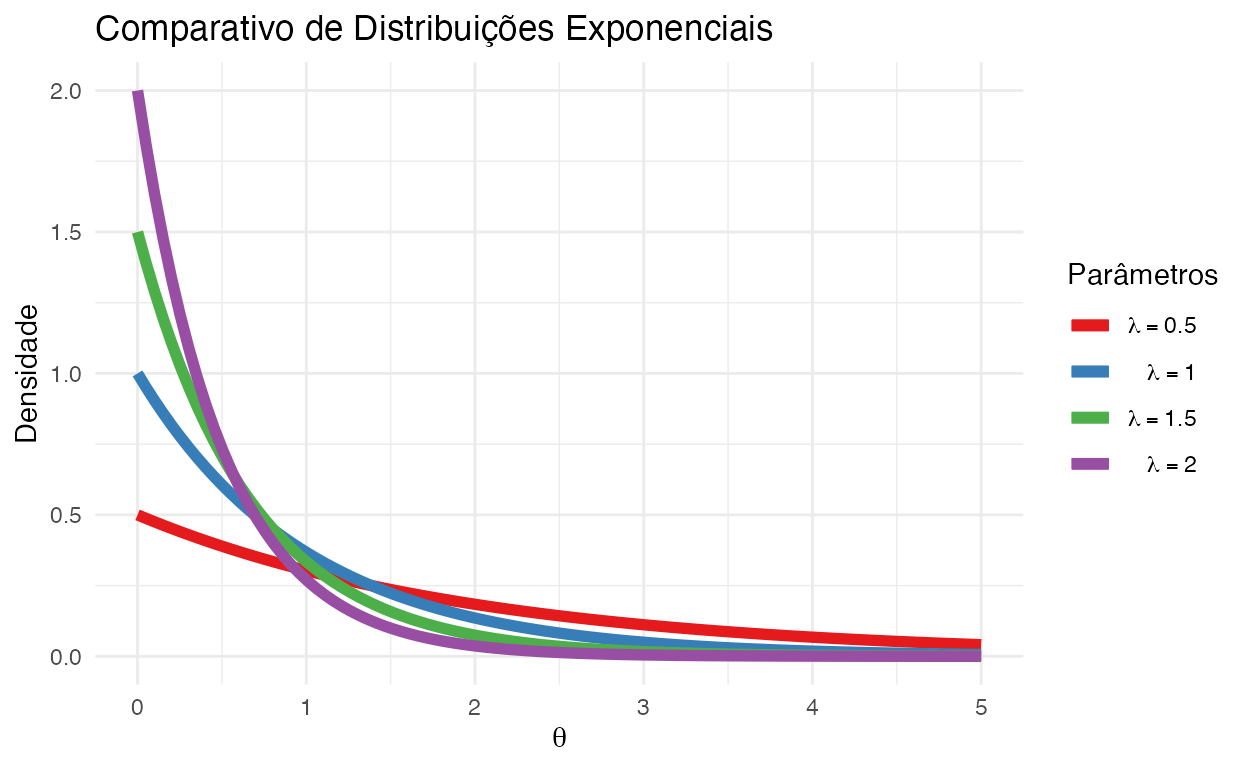
Figure 7: Comparativo de Distribuições Exponenciais

Distribuição $t$ de Student

A distribuição $t$ de Student surge ao estimar a média de uma população normalmente distribuída em situações onde o tamanho da amostra é pequeno e o desvio padrão da população é desconhecido.

Se tomarmos uma amostra de $n$ observações de uma distribuição normal, então a distribuição $t$ com $\nu = n-1$ graus de liberdade pode ser definida como a distribuição da localização da média da amostra em relação à média verdadeira, dividida pela desvio padrão da amostra, após multiplicar pelo termo padronizador $\sqrt{n}$ .

A distribuição $t$ é simétrica e em forma de sino, como a distribuição normal, mas tem caudas mais longas, o que significa que é mais propensa a produzir valores que estão longe de sua média.

A distribuição $t$ de Student possui um parâmetro e sua notação é $\text{Student} (\nu)$ :

Graus de Liberdade ( $\nu$ ): controla o quanto ela se assemelha com uma distribuição normal

Exemplo: Uma base de dados cheia de outliers.

ggplot(data = tibble(x = seq(-4, 4, length = 100))) +
  labs(
    title = "Comparativo de Distribuições t de Student",
    x = expression(theta),
    y = "Densidade",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dt(x, df = 1), color = "nu ==  1"), size = 2) +
  geom_line(aes(x, y = dt(x, df = 3), color = "nu ==  3"), size = 2) +
  geom_line(aes(x, y = dt(x, df = 8), color = "nu ==  8"), size = 2) +
  geom_line(aes(x, y = dt(x, df = 30), color = "nu ==  30"), size = 2) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

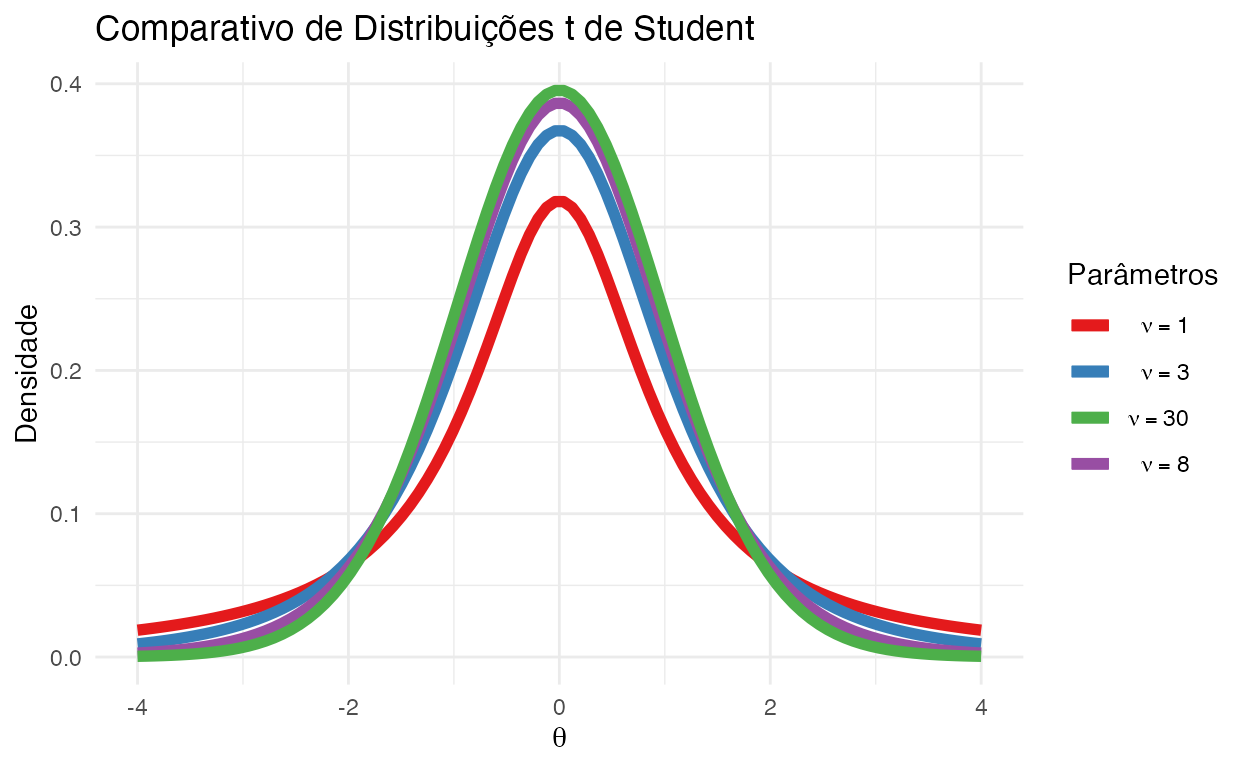
Figure 8: Comparativo de Distribuições $t$ de Student

Distribuição Beta

A distribuição beta é uma escolha natural para modelar qualquer coisa que seja restrita a valores entre 0 e 1. Portanto, é uma boa candidata para probabilidades e proporções.

A distribuição beta possui dois parâmetros e sua notação é $\text{Beta} (a, b)$ :

Parâmetro de Forma ( $a$ ou às vezes $\alpha$ ): controla o quanto a forma é deslocada para próximo de 1
Parâmetro de Forma ( $b$ ou às vezes $\beta$ ): controla o quanto a forma é deslocada para próximo de 0

Exemplo: Um jogador de basquete já marcou 5 lances livres e errou 3 em um total de 8 tentativas - $\text{Beta}(3, 5)$

ggplot(data = tibble(x = seq(0, 1, length = 100))) +
  labs(
    title = "Comparativo de Distribuições Beta",
    x = expression(theta),
    y = "Densidade",
    color = "Parâmetros"
  ) +
  geom_line(aes(x, y = dbeta(x, shape1 = 1, shape2 = 1), color = "list(alpha, beta) ==  1"), size = 2) +
  geom_line(aes(x, y = dbeta(x, shape1 = 3, shape2 = 2), color = "list(alpha ==  3, beta ==  2)"), size = 2) +
  geom_line(aes(x, y = dbeta(x, shape1 = 2, shape2 = 3), color = "list(alpha ==  2, beta ==  3)"), size = 2) +
  scale_color_brewer(palette = "Set1",
    labels = scales::label_parse())

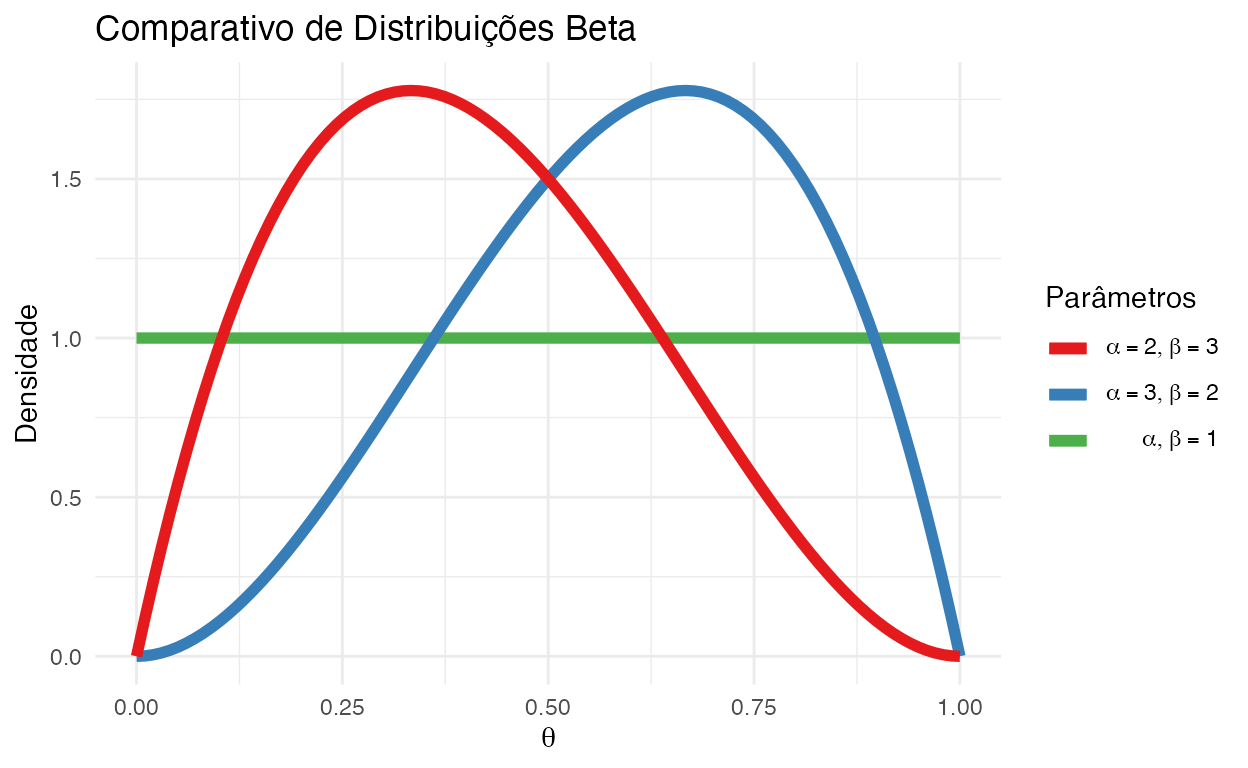
Figure 9: Comparativo de Distribuições Beta

Dashboard de Distribuições

Não cobrimos todas as distribuições existentes. Há uma pletora de distribuições probabilísticas.

Para acessar todo o zoológico de distribuições use essa ferramenta do Ben Lambert (estatístico do Imperial College of London): https://ben18785.shinyapps.io/distribution-zoo/

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] brms_2.15.0     rstanarm_2.21.1 Rcpp_1.0.6      skimr_2.1.3    
 [5] readr_1.4.0     readxl_1.3.1    tibble_3.1.2    ggplot2_3.3.3  
 [9] patchwork_1.1.1 cowplot_1.1.1  

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         repr_1.1.3           splines_4.1.0       
  [7] crosstalk_1.1.1      rstantools_2.1.1     inline_0.3.19       
 [10] digest_0.6.27        htmltools_0.5.1.1    magick_2.7.2        
 [13] rsconnect_0.8.18     fansi_0.5.0          magrittr_2.0.1      
 [16] RcppParallel_5.1.4   matrixStats_0.59.0   xts_0.12.1          
 [19] prettyunits_1.1.1    colorspace_2.0-1     textshaping_0.3.4   
 [22] xfun_0.23            dplyr_1.0.6          callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] gtable_0.3.0         V8_3.4.2             pkgbuild_1.2.0      
 [34] rstan_2.21.2         abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] xtable_1.8-4         stats4_4.1.0         StanHeaders_2.21.0-7
 [43] DT_0.18              htmlwidgets_1.5.3    threejs_0.3.3       
 [46] RColorBrewer_1.1-2   ellipsis_0.3.2       pkgconfig_2.0.3     
 [49] loo_2.4.1            farver_2.1.0         sass_0.4.0          
 [52] utf8_1.2.1           tidyselect_1.1.1     labeling_0.4.2      
 [55] rlang_0.4.11         reshape2_1.4.4       later_1.2.0         
 [58] munsell_0.5.0        cellranger_1.1.0     tools_4.1.0         
 [61] cli_2.5.0            generics_0.1.0       ggridges_0.5.3      
 [64] evaluate_0.14        stringr_1.4.0        fastmap_1.1.0       
 [67] yaml_2.2.1           ragg_1.1.2           processx_3.5.2      
 [70] knitr_1.33           purrr_0.3.4          nlme_3.1-152        
 [73] mime_0.10            projpred_2.0.2       xml2_1.3.2          
 [76] compiler_4.1.0       bayesplot_1.8.0      shinythemes_1.2.0   
 [79] rstudioapi_0.13      curl_4.3.1           gamm4_0.2-6         
 [82] png_0.1-7            bslib_0.2.5.1        stringi_1.6.2       
 [85] highr_0.9            ps_1.6.0             Brobdingnag_1.2-6   
 [88] lattice_0.20-44      Matrix_1.3-3         nloptr_1.2.2.2      
 [91] markdown_1.1         shinyjs_2.0.0        vctrs_0.3.8         
 [94] pillar_1.6.1         lifecycle_1.0.0      jquerylib_0.1.4     
 [97] bridgesampling_1.1-2 httpuv_1.6.1         R6_2.5.0            
[100] bookdown_0.22        promises_1.2.0.1     gridExtra_2.3       
[103] codetools_0.2-18     distill_1.2          boot_1.3-28         
[106] colourpicker_1.1.0   MASS_7.3-54          gtools_3.8.2        
[109] assertthat_0.2.1     rprojroot_2.0.2      withr_2.4.2         
[112] shinystan_2.5.0      mgcv_1.8-35          parallel_4.1.0      
[115] hms_1.1.0            grid_4.1.0           tidyr_1.1.3         
[118] coda_0.19-4          minqa_1.2.4          rmarkdown_2.8       
[121] downlit_0.2.1        shiny_1.6.0          lubridate_1.7.10    
[124] base64enc_0.1-3      dygraphs_1.1.1.6

References

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2013). Bayesian Data Analysis. Chapman and Hall/CRC.

Gelman, A., Hill, J., & Vehtari, A. (2020). Regression and other stories. Cambridge University Press.

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY-SA 4.0. Source code is available at https://github.com/storopoli/Estatistica-Bayesiana, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Storopoli (2021, Aug. 1). Estatística Bayesiana com R e Stan: Distribuições Estatísticas. Retrieved from https://storopoli.github.io/Estatistica-Bayesiana/2-Distribuicoes_Estatisticas.html

BibTeX citation

@misc{storopoli2021distsstatR,
  author = {Storopoli, Jose},
  title = {Estatística Bayesiana com R e Stan: Distribuições Estatísticas},
  url = {https://storopoli.github.io/Estatistica-Bayesiana/2-Distribuicoes_Estatisticas.html},
  year = {2021}
}

Distribuições Estatísticas

Author

Affiliation

Published

Citation

Discretas

Uniforme Discreta

Bernoulli

Binomial

Poisson

Binomial Negativa

Contínuas

Normal / Gaussiana

Log-normal

Exponencial

Distribuição tt de Student

Distribuição Beta

Dashboard de Distribuições

Ambiente

Footnotes

References

Corrections

Reuse

Citation

Distribuição $t$ de Student