Estatística Bayesiana com R e Stan: Regressão Logística Bayesiana

Jose Storopoli

Saindo do universo dos modelos lineares, começamos a nos aventurar nos modelos linares generalizados (generalized linear models – GLM). O primeiro deles é a regressão logística (também chamada de regressão binomial).

Uma regressão logística se comporta exatamente como um modelo linear: faz uma predição simplesmente computando uma soma ponderada das variáveis independentes $\mathbf{X}$ pelos coeficientes estimados $\boldsymbol{\beta}$, mais uma constante $\alpha$. Porém ao invés de retornar um valor contínuo $\boldsymbol{y}$, como a regressão linear, retorna a função logística desse valor:

\[ \text{Logística}(x) = \frac{1}{1 + e^{(-x)}} \]

Usamos regressão logística quando a nossa variável dependente é binária. Ela possui apenas dois valores distintos, geralmente codificados como $0$ ou $1$. Veja a figura 1 para uma intuição gráfica da função logística:

ggplot(data = tibble(
  x = seq(-10, 10, length.out = 100),
  y =  1 / (1 + exp(-x))
  ),
  aes(x, y)) +
  geom_line(size = 2, color = "steelblue") +
  ylab("Logística(x)")

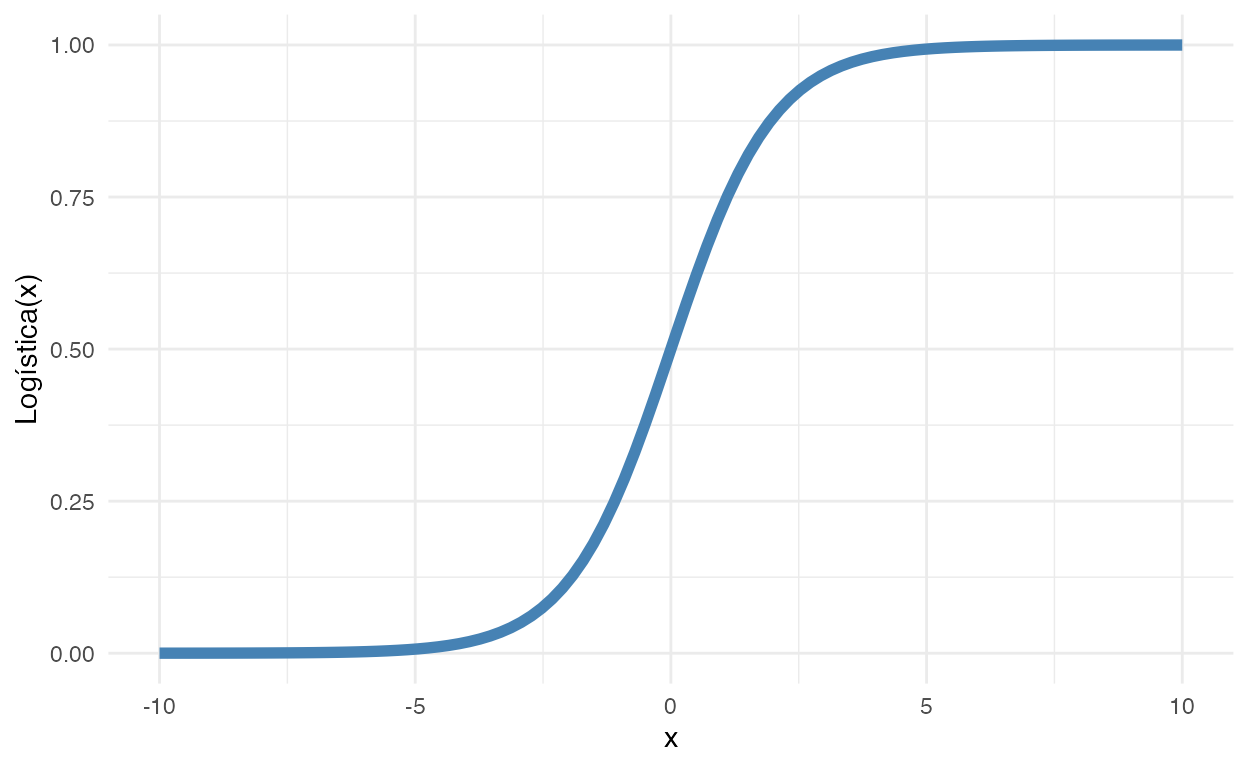
Figure 1: Função Logística

Como podemos ver, a função logística é basicamente um mapeamento de qualquer número real para um número real no intervalo entre 0 e 1:

\[ \text{Logística}(x) = \{ \mathbb{R} \in [- \infty , + \infty] \} \to \{ \mathbb{R} \in (0, 1) \} \]

Ou seja, a função logística é a candidata ideal para quando precisamos converter algo contínuo sem restrições para algo contínuo restrito entre 0 e 1. Por isso ela é usada quando precisamos que um modelo tenha como variável dependente uma probabilidade (lembrando que qualquer numero real entre 0 e 1 é uma probabilidade válida). No caso de uma variável dependente binária, podemos usar essa probabilidade como a chance da variável dependente tomar valor de 0 ou de 1.

Comparativo com a Regressão Linear

A regressão linear segue a seguinte formulação matemática:

\[ \text{Linear} = \alpha + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_k x_k \]

$\alpha$ - constante
$\boldsymbol{\beta} = \beta_1, \beta_2, \dots, \beta_k$ - coeficientes das variáveis independentes $x_1, x_2, \dots, x_k$
$k$ - número de variáveis independentes

Se você implementar uma pequena gambiarra matemática, você terá a regressão logística:

$\hat{p} = \text{Logística}(\text{Linear}) = \frac{1}{1 + e^{-\operatorname{Linear}}}$ - probabilidade prevista da observação ser o valor $1$
$\hat{y} = \begin{cases} 0 & \text { se } \hat{p} < 0.5 \\ 1 & \text { se } \hat{p} \geq 0.5 \end{cases}$ - previsão do valor discreto de $\boldsymbol{y}$

Exemplo:

\[\text{Previsão de Morte} = \text{Logística} \big(-10 + 10 \cdot \text{cancer} + 12 \cdot \text{diabetes} + 8 \cdot \text{obesidade} \big)\]

Regressão Logística Bayesiana

Podemos modelar regressão logística de duas maneiras. A primeira opção com uma função verossimilhança Bernoulli e a segunda opção com uma função verossimilhança binomial.

Com a verossimilhança Bernoulli modelamos uma variável dependente binária $\boldsymbol{y}$ que é o resultado de um experimento de Bernoulli com uma certa probabilidade $p$.

Já na verossimilhança binomial modelamos uma variável dependente contínua $\boldsymbol{y}$ que é o número de sucessos de $n$ experimentos Bernoulli independentes.

Usando Verossimilhança Bernoulli

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Bernoulli}\left( p\right) \\ p &\sim \text{Logística}(\alpha + \mathbf{X} \boldsymbol{\beta}) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \end{aligned} \]

Sendo que:

$\boldsymbol{y}$ – variável dependente binária
$p$ – probabilidade de $\boldsymbol{y}$ tomar o valor de $\boldsymbol{y}$ - sucesso de um experimento Bernoulli independente
$\text{Logística}$ – função logística
$\alpha$ – constante (também chamada de intercept)
$\boldsymbol{\beta}$ – vetor de coeficientes
$\mathbf{X}$ – matriz de dados

Usando Verossimilhança Binomial

\[ \begin{aligned} \boldsymbol{y} &\sim \text{Binomial}\left(n, p\right) \\ p &\sim \text{Logística}(\alpha + \mathbf{X} \boldsymbol{\beta}) \\ \alpha &\sim \text{Normal}(\mu_\alpha, \sigma_\alpha) \\ \boldsymbol{\beta} &\sim \text{Normal}(\mu_{\boldsymbol{\beta}}, \sigma_{\boldsymbol{\beta}}) \end{aligned} \]

Sendo que:

$\boldsymbol{y}$ – variável dependente contínua - sucessos de $n$ experimentos Bernoulli independentes
$n$ – número de experimentos Bernoulli independentes
$p$ – probabilidade de $\boldsymbol{y}$ tomar o valor de $\boldsymbol{y}$ - sucesso de um experimento Bernoulli
$\text{Logística}$ – função logística
$\alpha$ – constante (também chamada de intercept)
$\boldsymbol{\beta}$ – vetor de coeficientes
$\mathbf{X}$ – matriz de dados

Em ambas famílias de verossimilhança, o que falta é especificar quais são as prioris dos parâmetros do modelo:

Distribuição priori de $\alpha$ – Conhecimento que temos da constante do modelo
Distribuição priori de $\boldsymbol{\beta}$ – Conhecimento que temos dos coeficientes das variáveis independentes do modelo

Stan instanciará um modelo bayesiano com os dados fornecidos ($\boldsymbol{y}$ e $\mathbf{X}$) e encontrará a distribuição posterior dos parâmetros de interesse do modelo ($\alpha$ e $\boldsymbol{\beta}$) calculando a distribuição posterior completa de:

\[ P(\boldsymbol{\theta} \mid \boldsymbol{y}) = P(\alpha, \boldsymbol{\beta} \mid \boldsymbol{y}) \]

Regressão Logística com o `rstanarm` e `brms`

O rstanarm e brms podem tolerar qualquer modelo linear generalizado e regressão logística não é uma exceção. Não há função de verossimilhança Bernoulli em Stan (e, consequentemente, em nenhuma de suas interfaces) pois ela é apenas um caso especial da função de verossimilhança binomial com apenas um único experimento Bernoulli. Ou seja:

\[ \text{Bernouli}(p) = \text{Binomial}(1, p) \]

Para designar um modelo binomial no rstanarm e brms é preciso simplesmente alterar o argumento family da função stan_glm() ou brm(). Isso faz com que a família da função de verossimilhança do modelo seja modificada. Você pode controlar também a função de ligação com argumento link mas acredito que para a vasta maioria dos casos não é necessário alterar o padrão que Stan usa para as diferentes famílias de funções de verossimilhança.

Exemplo - Propensão a mudar de poço de água contaminado

Para exemplo, usaremos um dataset chamado wells (Gelman & Hill, 2007) que está incluído no rstanarm. É uma survey com 3.200 residentes de uma pequena área de Bangladesh na qual os lençóis freáticos estão contaminados por arsênico. Respondentes com altos níveis de arsênico nos seus poços foram encorajados para trocar a sua fonte de água para uma níveis seguros de arsênico.

Possui as seguintes variáveis:

switch: dependente indicando se o respondente trocou ou não de poço
arsenic: nível de arsênico do poço do respondente
dist: distância em metros da casa do respondente até o poço seguro mais próximo
association: dummy se os membros da casa do respondente fazem parte de alguma organização da comunidade
educ: quantidade de anos de educação que o chefe da família respondente possui

options(mc.cores = parallel::detectCores())
options(Ncpus = parallel::detectCores())

library(rstanarm)
data(wells)

Descritivo das variáveis

Antes de tudo, analise SEMPRE os dados em mãos. Graficamente e com tabelas. Isso pode ajudar a elucidar prioris além de embasar melhor conhecimento de domínio do fenômeno de interesse.

Pessoalmente uso o pacote skimr (Waring et al., 2021) com a função skim():

library(skimr)

skim(wells)

Table 1: Data summary
Name	wells
Number of rows	3020
Number of columns	5
_______________________
Column type frequency:
numeric	5
________________________
Group variables	None

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
switch	1	0.58	0.49	0.00	0.00	1.0	1.0	1.0	▆▁▁▁▇
arsenic	1	1.66	1.11	0.51	0.82	1.3	2.2	9.7	▇▂▁▁▁
dist	1	48.33	38.48	0.39	21.12	36.8	64.0	339.5	▇▂▁▁▁
assoc	1	0.42	0.49	0.00	0.00	0.0	1.0	1.0	▇▁▁▁▆
educ	1	4.83	4.02	0.00	0.00	5.0	8.0	17.0	▇▇▅▁▁

Modelo Binomial

O modelo possuirá as seguintes variáveis como independentes: dist,arsenic, assoc e educ. Para todas essas variáveis, como os coeficientes estarão em uma escala logit (que é o inverso da transformação logística), usarei uma priori de uma distribuição normal com média 0 e desvio padrão 2.5. O que resulta em prior = normal(0, 2.5). Vou colocar a priori da constante $\alpha$ como uma normal centrada em 0 e com um desvio padrão 2.5, basicamente traduzindo o que usamos como priori em modelos gaussianos (regressão linear). Isto resulta em prior_intercept = normal(0, 2.5). Notem que aqui não temos erro do modelo, pois a função de verossimilhança não faz pressupostos sobre desvios como era o caso na regressão linear com uma verossimilhança Gaussiana/Normal. Portanto não há o que se especificar para prior_aux.

model_binomial <- stan_glm(
  switch ~ dist + arsenic + assoc + educ,
  data = wells,
  family = binomial,
  prior = normal(0, 2.5),
  prior_intercept = normal(0, 2.5)
)

Vamos ver como ficaram as estimação dos parâmetros de interesse do modelo com summary():

summary(model_binomial)


Model Info:
 function:     stan_glm
 family:       binomial [logit]
 formula:      switch ~ dist + arsenic + assoc + educ
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 3020
 predictors:   5

Estimates:
              mean   sd   10%   50%   90%
(Intercept) -0.2    0.1 -0.3  -0.2   0.0 
dist         0.0    0.0  0.0   0.0   0.0 
arsenic      0.5    0.0  0.4   0.5   0.5 
assoc       -0.1    0.1 -0.2  -0.1   0.0 
educ         0.0    0.0  0.0   0.0   0.1 

Fit Diagnostics:
           mean   sd   10%   50%   90%
mean_PPD 0.6    0.0  0.6   0.6   0.6  

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.0  1.0  3655 
dist          0.0  1.0  3518 
arsenic       0.0  1.0  2853 
assoc         0.0  1.0  3460 
educ          0.0  1.0  3419 
mean_PPD      0.0  1.0  3312 
log-posterior 0.0  1.0  1781 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Não tivemos nenhum problema nas correntes Markov pois todos os Rhat estão bem abaixo de 1.01.

Vamos verificar o Posterior Predictive Check do modelo binomial na figura 2:

pp_check(model_binomial)

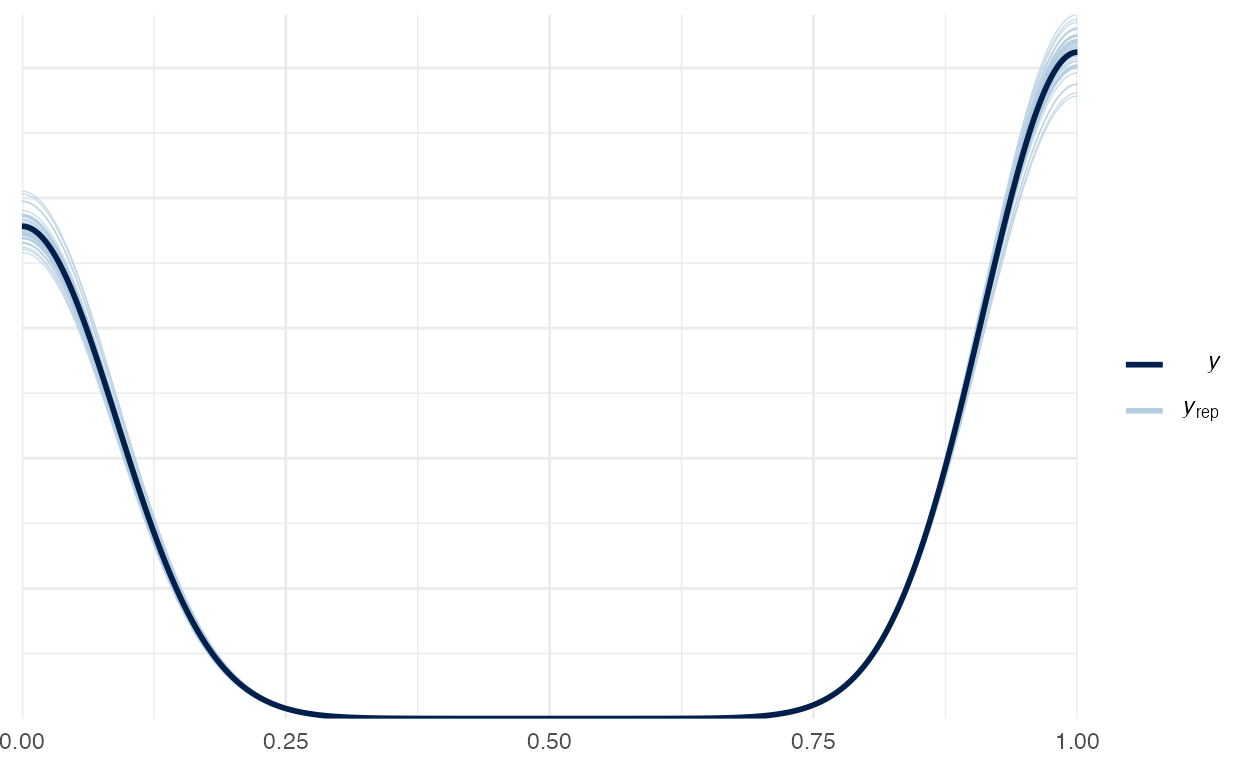
Figure 2: Posterior Preditive Check do modelo binomial

Este é um ótimo exemplo de um Posterior Predictive Check no qual não conseguimos identificar qualquer anomalia no modelo.

Interpretação dos coeficientes

Ao vermos a fórmula de regressão logística percebemos a interpretação dos coeficientes requer uma transformação. A transformação que precisamos fazer á a que inverte a função logística. Mas antes preciso falar sobre qual a diferença matemática entre probabilidade (em inglês probability) e chances (em inglês odds). Probabilidade já discutimos na Aula 0 - O que é Estatística Bayesiana?: um número real entre 0 e 1 que representa a certeza de que um evento irá acontecer por meio de frequências de longo-prazo (probabilidade frequentista) ou níveis de credibilidade (probabilidade Bayesiana). Chances é um número positivo real ($\mathbb{R}^+$) que mensura também a certeza de um evento. Mas essa certeza não é expressa como uma probabilidade (algo entre 0 e 1), mas como uma razão entre a quantidade de resultados que produzem o evento desejado e a quantidade de resultados que não produzem o evento desejado:

\[ \text{Chances} = \frac{p}{1-p} \]

onde $p$ é a probabilidade. Chance com o valor de $1$ é uma chance neutra, algo como uma moeda justa $p = \frac{1}{2}$. Chances abaixo de $1$ decrescem a probabilidade de vermos um certo evento e chances acima de $1$ aumentam a probabilidade do evento. É um sistema de quantificação de incerteza muito usado em casas de apostas. Chances 2:1 quer dizer que a casa de aposta pagará R$ 2 para cada R$ 1 apostado caso o evento apostado ocorra.

Se você revisitar a função logística, verá que ela os coeficientes de $\boldsymbol{\beta}$ são literalmente o logarítmo da chance (em inglês logodds):

\[ \begin{aligned} p &\sim \text{Logística}(\alpha + \mathbf{X} \boldsymbol{\beta} ) \\ p &\sim \text{Logística}(\alpha) + \text{Logística}( \mathbf{X} \boldsymbol{\beta}) \\ \boldsymbol{\beta} &= \frac{1}{1 + e^{(-\boldsymbol{\beta})}}\\ \boldsymbol{\beta} &= \log(\text{Chance}) \end{aligned} \]

Portanto, os coeficientes de uma regressão logística são expressados em logodds no qual $0$ é o elemento neutro e qualquer número acima ou abaixo aumenta ou diminui as chances de obtermos um “sucesso” de $\boldsymbol{y}$. Para termos uma interpretação mais intuitiva (igual a das casas de apostas) precisamos converter as logodds em chances revertendo a função $\log$. Para isso basta “exponenciar” os valores de $\boldsymbol{\beta}$:

\[ \text{Chances} = e^{\boldsymbol{\beta}} \]

Fazemos isso com a função exp() do R nos coeficientes do model_binomial:

coeff <- exp(model_binomial$coefficients)
coeff

(Intercept)        dist     arsenic       assoc        educ 
       0.85        0.99        1.60        0.88        1.04

(Intercept): a chance basal de respondentes mudarem de poço (14% de não mudarem)
dist: a cada metro de distância diminui a chance de troca de poço em 1%
arsenic: a cada incremento do nível de arsênico aumenta a chance de troca de poço em 60%
assoc: residências com membros que fazem parte de alguma organização da comunidade diminui a chance de troca de poço em 12%
educ: a cada incremento dos anos de estudo aumenta a chance de troca de poço em 4%

Atividade Prática

Dois datasets estão disponíveis no diretório datasets/:

Titanic Survival: datasets/Titanic_Survival.csv
IBM HR Analytics Employee Attrition & Performance: datasets/IBM_HR_Attrition.csv

###

Ambiente

sessionInfo()

R version 4.1.0 (2021-05-18)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur 10.16

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.1/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods  
[7] base     

other attached packages:
 [1] gapminder_0.3.0      ggExtra_0.9          dplyr_1.0.6         
 [4] rstan_2.21.2         StanHeaders_2.21.0-7 MASS_7.3-54         
 [7] ggforce_0.3.3        gganimate_1.0.7      plotly_4.9.3        
[10] carData_3.0-4        DiagrammeR_1.0.6.1   brms_2.15.0         
[13] rstanarm_2.21.1      Rcpp_1.0.6           skimr_2.1.3         
[16] readr_1.4.0          readxl_1.3.1         tibble_3.1.2        
[19] ggplot2_3.3.3        patchwork_1.1.1      cowplot_1.1.1       

loaded via a namespace (and not attached):
  [1] backports_1.2.1      systemfonts_1.0.2    plyr_1.8.6          
  [4] igraph_1.2.6         lazyeval_0.2.2       repr_1.1.3          
  [7] splines_4.1.0        crosstalk_1.1.1      rstantools_2.1.1    
 [10] inline_0.3.19        digest_0.6.27        htmltools_0.5.1.1   
 [13] magick_2.7.2         rsconnect_0.8.18     fansi_0.5.0         
 [16] magrittr_2.0.1       RcppParallel_5.1.4   matrixStats_0.59.0  
 [19] xts_0.12.1           prettyunits_1.1.1    colorspace_2.0-1    
 [22] textshaping_0.3.4    xfun_0.23            callr_3.7.0         
 [25] crayon_1.4.1         jsonlite_1.7.2       lme4_1.1-27         
 [28] survival_3.2-11      zoo_1.8-9            glue_1.4.2          
 [31] polyclip_1.10-0      gtable_0.3.0         V8_3.4.2            
 [34] pkgbuild_1.2.0       abind_1.4-5          scales_1.1.1        
 [37] mvtnorm_1.1-1        DBI_1.1.1            miniUI_0.1.1.1      
 [40] isoband_0.2.4        progress_1.2.2       viridisLite_0.4.0   
 [43] xtable_1.8-4         tmvnsim_1.0-2        stats4_4.1.0        
 [46] DT_0.18              httr_1.4.2           htmlwidgets_1.5.3   
 [49] threejs_0.3.3        RColorBrewer_1.1-2   ellipsis_0.3.2      
 [52] pkgconfig_2.0.3      loo_2.4.1            farver_2.1.0        
 [55] sass_0.4.0           here_1.0.1           utf8_1.2.1          
 [58] tidyselect_1.1.1     labeling_0.4.2       rlang_0.4.11        
 [61] reshape2_1.4.4       later_1.2.0          visNetwork_2.0.9    
 [64] munsell_0.5.0        cellranger_1.1.0     tools_4.1.0         
 [67] cli_2.5.0            generics_0.1.0       gifski_1.4.3-1      
 [70] ggridges_0.5.3       evaluate_0.14        stringr_1.4.0       
 [73] fastmap_1.1.0        yaml_2.2.1           ragg_1.1.2          
 [76] processx_3.5.2       knitr_1.33           purrr_0.3.4         
 [79] nlme_3.1-152         mime_0.10            projpred_2.0.2      
 [82] xml2_1.3.2           compiler_4.1.0       bayesplot_1.8.0     
 [85] shinythemes_1.2.0    rstudioapi_0.13      curl_4.3.1          
 [88] gamm4_0.2-6          png_0.1-7            tweenr_1.0.2        
 [91] bslib_0.2.5.1        stringi_1.6.2        highr_0.9           
 [94] ps_1.6.0             Brobdingnag_1.2-6    lattice_0.20-44     
 [97] Matrix_1.3-3         nloptr_1.2.2.2       markdown_1.1        
[100] shinyjs_2.0.0        vctrs_0.3.8          pillar_1.6.1        
[103] lifecycle_1.0.0      jquerylib_0.1.4      bridgesampling_1.1-2
[106] data.table_1.14.0    httpuv_1.6.1         R6_2.5.0            
[109] bookdown_0.22        promises_1.2.0.1     gridExtra_2.3       
[112] codetools_0.2-18     distill_1.2          boot_1.3-28         
[115] colourpicker_1.1.0   gtools_3.8.2         assertthat_0.2.1    
[118] rprojroot_2.0.2      withr_2.4.2          mnormt_2.0.2        
[121] shinystan_2.5.0      mgcv_1.8-35          parallel_4.1.0      
[124] hms_1.1.0            grid_4.1.0           tidyr_1.1.3         
[127] coda_0.19-4          minqa_1.2.4          rmarkdown_2.8       
[130] downlit_0.2.1        shiny_1.6.0          lubridate_1.7.10    
[133] base64enc_0.1-3      dygraphs_1.1.1.6

Gelman, A., & Hill, J. (2007). Data analysis using regression and multilevel/hierarchical models. Cambridge university press.

Waring, E., Quinn, M., McNamara, A., Arino de la Rubia, E., Zhu, H., & Ellis, S. (2021). Skimr: Compact and flexible summaries of data. Retrieved from https://CRAN.R-project.org/package=skimr

Regressão Logística Bayesiana

Comparativo com a Regressão Linear

Regressão Logística Bayesiana

Usando Verossimilhança Bernoulli

Usando Verossimilhança Binomial

Regressão Logística com o `rstanarm` e `brms`

Exemplo - Propensão a mudar de poço de água contaminado

Descritivo das variáveis

Modelo Binomial

Interpretação dos coeficientes

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Regressão Logística Bayesiana

Comparativo com a Regressão Linear

Regressão Logística Bayesiana

Usando Verossimilhança Bernoulli

Usando Verossimilhança Binomial

Regressão Logística com o rstanarm e brms

Exemplo - Propensão a mudar de poço de água contaminado

Descritivo das variáveis

Modelo Binomial

Interpretação dos coeficientes

Atividade Prática

Ambiente

References

Corrections

Reuse

Citation

Regressão Logística com o `rstanarm` e `brms`